- Déterminer son polynôme caractéristique.
- Diagonaliser la matrice
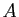 .
.
- Déterminer son polynôme minimal.
- Pour
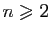 , donner une expression de
, donner une expression de 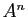 en fonction de
en fonction de 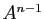 et
et 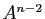 .
.
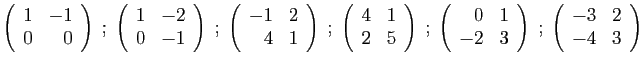
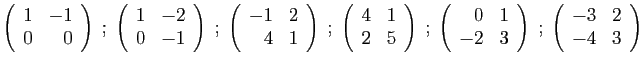
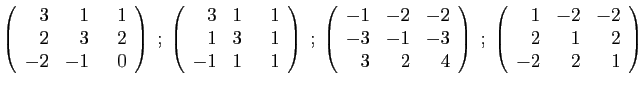
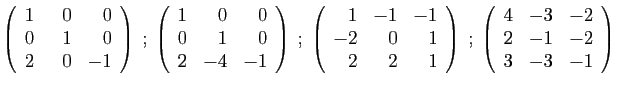
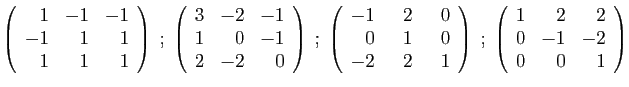

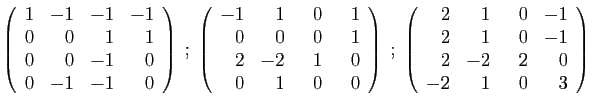
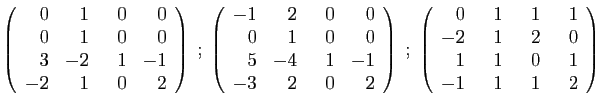
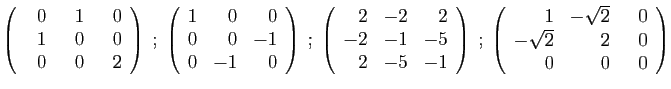
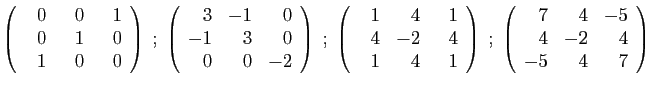
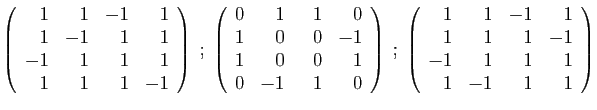
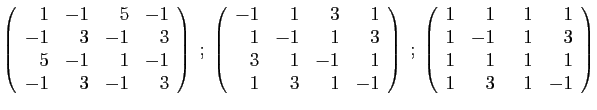
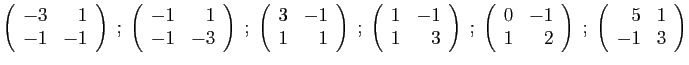
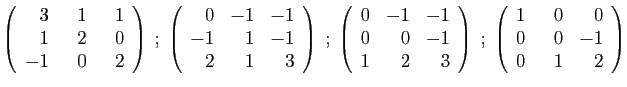
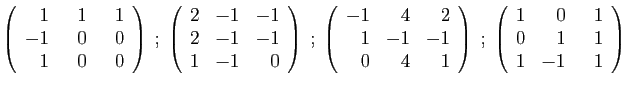
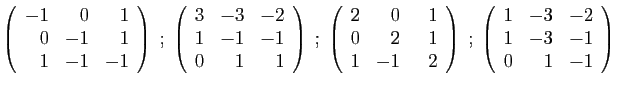
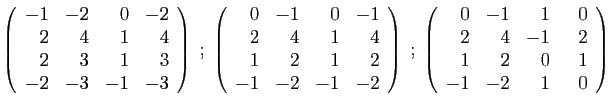
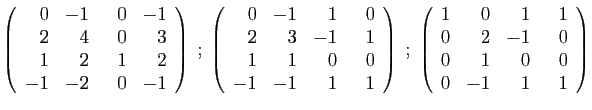
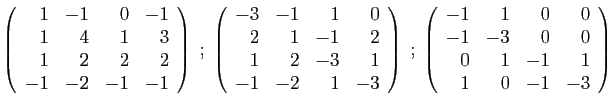
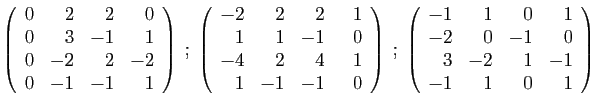
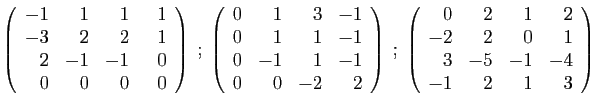
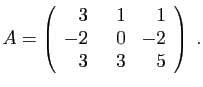
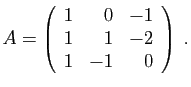
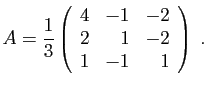
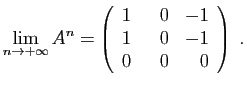
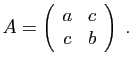
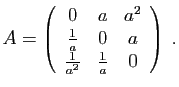
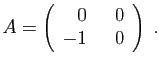
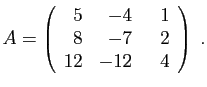
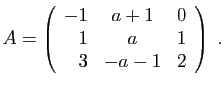
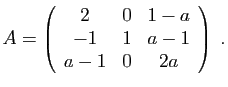
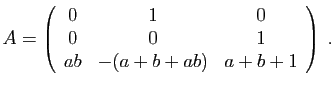
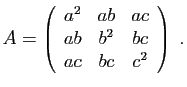
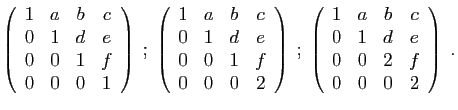
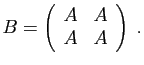
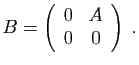
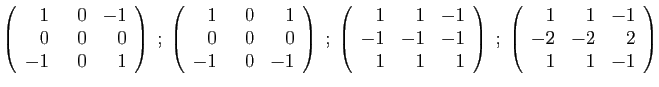
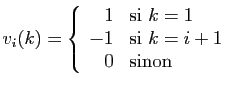
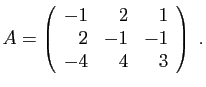
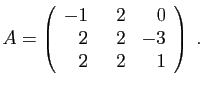
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales