Soient
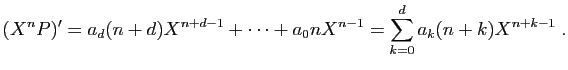
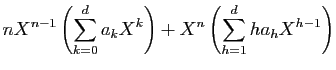 |
|||
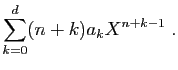 |
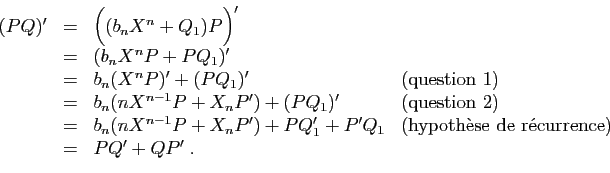
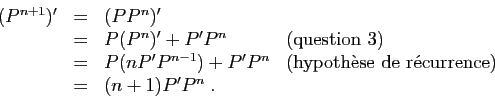
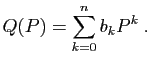
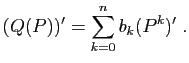
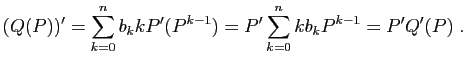
Soient
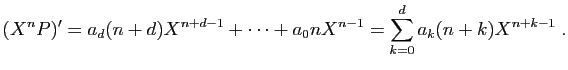
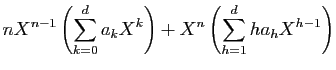 |
|||
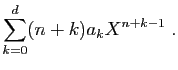 |
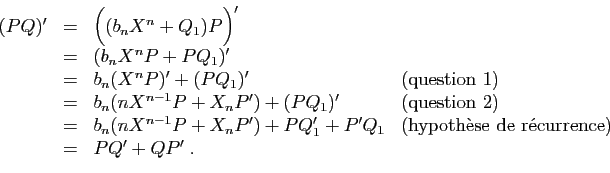
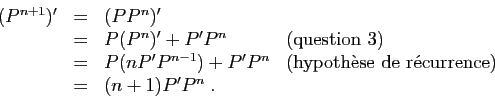
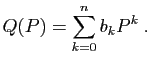
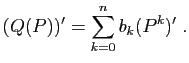
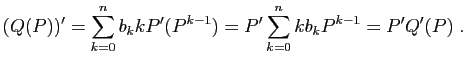
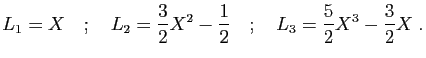
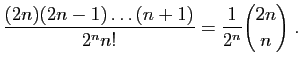
Prenons la dérivée ![]() -ième des deux membres, en utilisant
la formule de Leibniz. Pour le membre de gauche, on obtient :
-ième des deux membres, en utilisant
la formule de Leibniz. Pour le membre de gauche, on obtient :
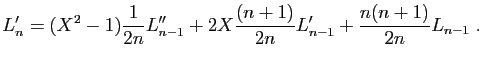
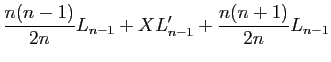 |
|||
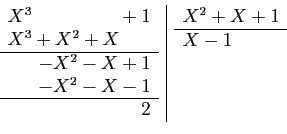
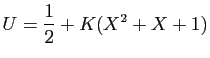 et
et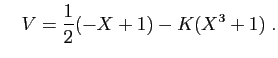
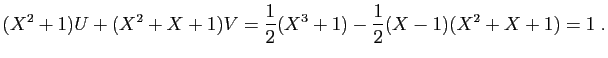
![$\displaystyle \left\{ \left(\frac{1}{2}+K(X^2+X+1)\;,\;
\frac{1}{2}(-X+1)-K(X^3+1)\right)\;,\quad K\in\mathbb{R}[X] \right\}\;.
$](img813.gif)
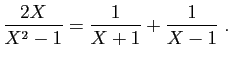
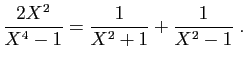
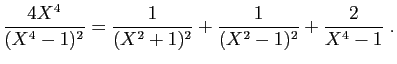
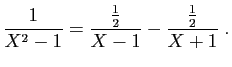
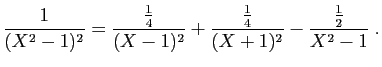
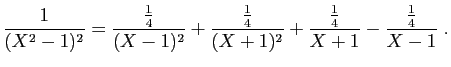
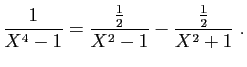
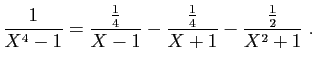
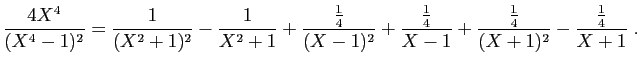
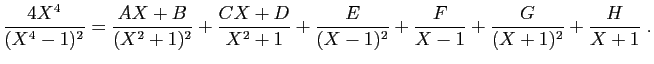
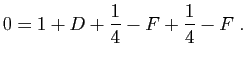
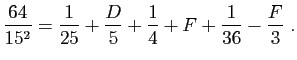
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales