L'objectif principal de cette section est
le théorème de décomposition en
éléments simples,
utilisé notamment pour le calcul des primitives de
fractions rationnelles, et qui est un peu indigeste.
Démonstration : Preuve de l'existence
Dans un premier temps, on va considérer les polynômes :
Chaque 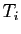 reprend les facteurs de la décomposition de
reprend les facteurs de la décomposition de
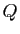 à l'exception de
à l'exception de 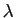 et
et
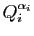 .
.
Un éventuel diviseur irréductible unitaire commun à
tous ces polynômes doit diviser 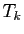 ; ce doit donc être un
des polynômes
; ce doit donc être un
des polynômes 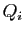 avec
avec 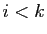 . Mais
. Mais 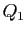 ne divise pas
ne divise pas 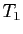 ,
, 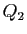 ne
divise pas
ne
divise pas 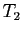 , et ce jusqu'à
, et ce jusqu'à 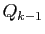 qui ne divise pas
qui ne divise pas 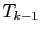 .
Les polynômes
.
Les polynômes 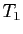 , ...,
, ..., 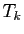 ne possèdent donc aucun diviseur
irréductible unitaire commun ; cela entraîne
qu'ils sont premiers entre eux.
ne possèdent donc aucun diviseur
irréductible unitaire commun ; cela entraîne
qu'ils sont premiers entre eux.
On peut donc écrire une identité de Bézout :
il existe des polynômes 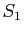 , ...,
, ..., 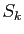 de
de
![$ \mathbb{K}[X]$](img126.gif) ,
tels que
,
tels que
Multiplions cette identité par
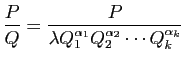 ;
on obtient :
;
on obtient :
donc
En notant 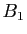 , ...,
, ..., 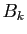 les divers
numérateurs qui interviennent dans la dernière formule, on a
donc réussi à écrire :
les divers
numérateurs qui interviennent dans la dernière formule, on a
donc réussi à écrire :
On va alors manipuler successivement chacun
des termes de cette addition. Fixons un 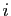 avec
avec
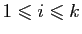 et travaillons l'expression
et travaillons l'expression
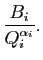
On commence par faire la division euclidienne
de 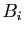 par
par 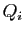 , en notant judicieusement le
quotient et le reste :
, en notant judicieusement le
quotient et le reste :
En reportant cette division euclidienne en
lieu et place de 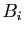 on a réécrit :
on a réécrit :
On recommence une division euclidienne, cette fois-ci de
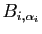 par
par 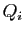 , en notant toujours opportunément quotient et reste :
, en notant toujours opportunément quotient et reste :
et on reporte de nouveau dans l'expression la plus fraîche de
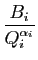 ; on obtient :
; on obtient :
On recommence jusqu'à ne plus pouvoir recommencer,
ce qui donne finalement une expression :
Il n'y a plus qu'à regrouper toutes ces expressions et à noter
pour avoir terminé la preuve d'existence.
Preuve de l'unicité
On l'écrira (peut-être) une prochaine fois,
elle n'est pas spécialement amusante.
Contrairement à la preuve d'existence,
il n'y a guère d'idées, seulement des décomptes de degrés. Pour comprendre cette décomposition, le mieux est d'examiner sa
forme sur un cas particulier, rassemblant les différentes
situations. Voici deux polynômes
Pour comprendre cette décomposition, le mieux est d'examiner sa
forme sur un cas particulier, rassemblant les différentes
situations. Voici deux polynômes 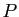 et
et 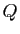 dans
dans
![$ \mathbb{R}[X]$](img249.gif) avec
avec 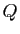 non nul, qui
définissent donc
une fraction rationnelle
non nul, qui
définissent donc
une fraction rationnelle 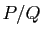 dans
dans
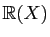 , et
la décomposition de
, et
la décomposition de 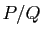 dans
dans
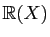 .
On choisit
.
On choisit
Alors,
où les lettres de 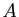 jusqu'à
jusqu'à 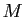 désignent des réels à
déterminer. La théorie assure que ces réels existent et sont
uniques. Il suffirait donc de réduire tous les éléments simples
au même dénominateur, et d'identifier les numérateurs
pour obtenir autant d'équations que d'inconnues (14 dans notre
cas). Ce n'est pas ainsi qu'on procède en pratique. On utilise
plusieurs techniques de manière à déterminer le plus de
coefficients possibles par des équations simples. Voici ces
techniques.
désignent des réels à
déterminer. La théorie assure que ces réels existent et sont
uniques. Il suffirait donc de réduire tous les éléments simples
au même dénominateur, et d'identifier les numérateurs
pour obtenir autant d'équations que d'inconnues (14 dans notre
cas). Ce n'est pas ainsi qu'on procède en pratique. On utilise
plusieurs techniques de manière à déterminer le plus de
coefficients possibles par des équations simples. Voici ces
techniques.
Pour la partie polynomiale
Celle-ci est non nulle seulement
dans le cas où le degré du numérateur est supérieur ou égal
au degré du dénominateur. Dans ce cas le polynôme cherché, que
l'on appelle la partie entière, est
le quotient 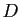 de la division euclidienne de
de la division euclidienne de 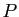 par
par 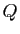 :
:
où le reste 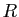 est de degré strictement
inférieur au degré de
est de degré strictement
inférieur au degré de 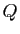 .
Dans notre exemple,
.
Dans notre exemple, 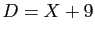 .
Il faut s'assurer auparavant que la fraction est bien irréductible,
et la simplifier éventuellement si elle ne l'était pas.
.
Il faut s'assurer auparavant que la fraction est bien irréductible,
et la simplifier éventuellement si elle ne l'était pas.
Pour les termes en
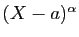 Si on multiplie les deux membres de la décomposition par
Si on multiplie les deux membres de la décomposition par
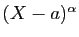 , la racine
, la racine 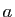 disparaît. On peut donc
remplacer
disparaît. On peut donc
remplacer 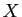 par
par 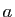 , ce qui annule tous les termes de la
décomposition sauf un. Il reste à
gauche une certaine valeur, que l'on calcule en général facilement.
Dans notre exemple, si on multiplie les deux membres par
, ce qui annule tous les termes de la
décomposition sauf un. Il reste à
gauche une certaine valeur, que l'on calcule en général facilement.
Dans notre exemple, si on multiplie les deux membres par 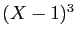 , et
qu'on remplace
, et
qu'on remplace 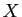 par
par 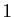 , on
trouve :
, on
trouve :
soit
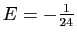 .
.
Pour les termes en
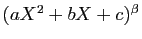
On procède de même, en remplaçant 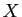 par
une des racines complexes du trinôme. Dans notre cas, on multiplie
les deux membres par
par
une des racines complexes du trinôme. Dans notre cas, on multiplie
les deux membres par 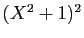 , et on remplace
, et on remplace 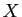 par
par
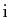 . On trouve :
. On trouve :
On identifie alors la partie réelle et la partie imaginaire :
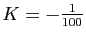 et
et
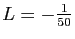 .
.
Pour les autres termes
Il faut chercher les équations les plus simples possibles, en
prenant des valeurs particulières pour 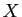 , qui ne soient pas des
racines du dénominateur (
, qui ne soient pas des
racines du dénominateur (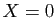 ,
, 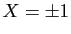 , etc...).
On peut aussi
penser à faire tendre
, etc...).
On peut aussi
penser à faire tendre 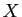 vers l'infini. On n'a recours à une
réduction au même dénominateur avec identification des
coefficients qu'en dernier ressort.
vers l'infini. On n'a recours à une
réduction au même dénominateur avec identification des
coefficients qu'en dernier ressort.
Voici un exemple plus simple, sur lequel nous allons détailler tous
les calculs.
Il s'agit de décomposer en éléments simples la fraction rationnelle
Le numérateur et le dénominateur sont premiers entre eux, la
fraction est bien irréductible.
Sa décomposition en éléments simples dans
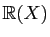 a la forme suivante.
a la forme suivante.
où les lettres de 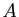 jusqu'à
jusqu'à 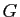 désignent des réels à déterminer.
La division euclidienne du numérateur par le dénominateur donne :
désignent des réels à déterminer.
La division euclidienne du numérateur par le dénominateur donne :
Donc 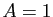 ,
, 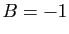 , et :
, et :
On peut désormais ne travailler que sur la partie restante, à
savoir :
On multiplie les deux membres par 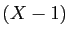 , et on remplace
, et on remplace 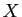 par
par
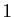 . On trouve
. On trouve
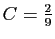 .
.
On multiplie ensuite les deux membres par
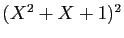 , et on
remplace
, et on
remplace 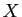 par
par
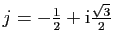 . On trouve
. On trouve
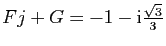 . En identifiant les parties réelles et
imaginaires, on trouve
. En identifiant les parties réelles et
imaginaires, on trouve
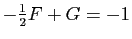 et
et
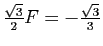 . La solution de ce système
de deux équations à deux inconnues est
. La solution de ce système
de deux équations à deux inconnues est
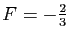 et
et
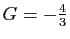 .
.
On peut ensuite remplacer 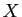 par
par
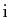 , et identifier partie réelle et
partie imaginaire. On trouve
, et identifier partie réelle et
partie imaginaire. On trouve
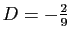 et
et
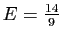 .
.
Une fois tout cela fait, il est bon de vérifier les calculs,
en utilisant une ou plusieurs valeurs
particulières.
Ainsi,
- pour
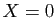 ,
, 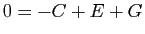 ,
,
- pour
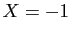 ,
,
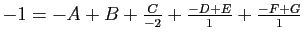 ,
,
- après avoir enlevé la partie entière, si on
multiplie les deux membres par
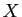 et qu'on fait tendre
et qu'on fait tendre 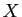 vers
vers
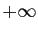 :
: 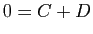 .
.
Voici donc la décomposition dans
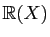 .
.
La décomposition dans
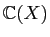 a une forme différente. Nous notons
encore
a une forme différente. Nous notons
encore
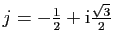 , de sorte que
, de sorte que 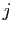 et
et
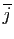 sont les deux racines de
sont les deux racines de 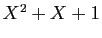 .
.
A priori, les lettres de 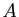 jusqu'à
jusqu'à 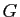 désignent des nombres
complexes, mais le fait que la
fraction initiale ait tous ses coefficients réels simplifie quelque
peu le problème : la décomposition ne doit pas changer si on prend
le conjugué des deux membres. L'unicité de cette décomposition
entraîne :
désignent des nombres
complexes, mais le fait que la
fraction initiale ait tous ses coefficients réels simplifie quelque
peu le problème : la décomposition ne doit pas changer si on prend
le conjugué des deux membres. L'unicité de cette décomposition
entraîne :
Les techniques de décomposition utilisées dans
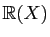 restent
valables. On trouve donc encore :
restent
valables. On trouve donc encore :
Nous laissons au lecteur le plaisir de calculer les autres
coefficients. La décomposition dans
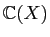 est la suivante :
est la suivante :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
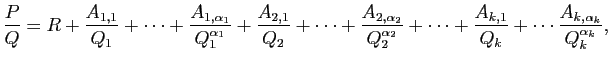
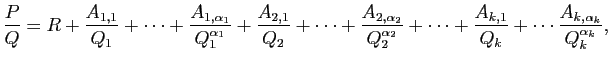
![]() ; ce doit donc être un
des polynômes
; ce doit donc être un
des polynômes ![]() avec
avec ![]() . Mais
. Mais ![]() ne divise pas
ne divise pas ![]() ,
, ![]() ne
divise pas
ne
divise pas ![]() , et ce jusqu'à
, et ce jusqu'à ![]() qui ne divise pas
qui ne divise pas ![]() .
Les polynômes
.
Les polynômes ![]() , ...,
, ..., ![]() ne possèdent donc aucun diviseur
irréductible unitaire commun ; cela entraîne
qu'ils sont premiers entre eux.
ne possèdent donc aucun diviseur
irréductible unitaire commun ; cela entraîne
qu'ils sont premiers entre eux.
![]() , ...,
, ..., ![]() de
de
![]() ,
tels que
,
tels que
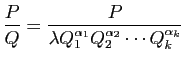 ;
on obtient :
;
on obtient :
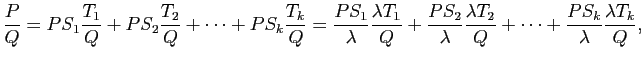
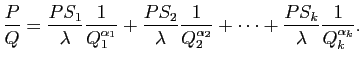
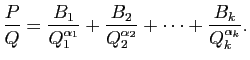
![]() par
par ![]() , en notant judicieusement le
quotient et le reste :
, en notant judicieusement le
quotient et le reste :
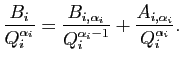
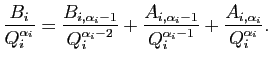
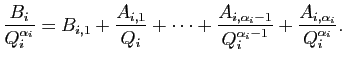
![]() Pour comprendre cette décomposition, le mieux est d'examiner sa
forme sur un cas particulier, rassemblant les différentes
situations. Voici deux polynômes
Pour comprendre cette décomposition, le mieux est d'examiner sa
forme sur un cas particulier, rassemblant les différentes
situations. Voici deux polynômes ![]() et
et ![]() dans
dans
![]() avec
avec ![]() non nul, qui
définissent donc
une fraction rationnelle
non nul, qui
définissent donc
une fraction rationnelle ![]() dans
dans
![]() , et
la décomposition de
, et
la décomposition de ![]() dans
dans
![]() .
On choisit
.
On choisit
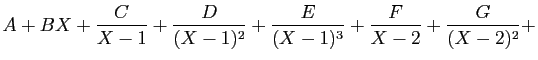
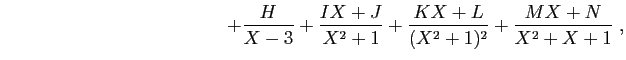
![]() de la division euclidienne de
de la division euclidienne de ![]() par
par ![]() :
:
![]() Si on multiplie les deux membres de la décomposition par
Si on multiplie les deux membres de la décomposition par
![]() , la racine
, la racine ![]() disparaît. On peut donc
remplacer
disparaît. On peut donc
remplacer ![]() par
par ![]() , ce qui annule tous les termes de la
décomposition sauf un. Il reste à
gauche une certaine valeur, que l'on calcule en général facilement.
Dans notre exemple, si on multiplie les deux membres par
, ce qui annule tous les termes de la
décomposition sauf un. Il reste à
gauche une certaine valeur, que l'on calcule en général facilement.
Dans notre exemple, si on multiplie les deux membres par ![]() , et
qu'on remplace
, et
qu'on remplace ![]() par
par ![]() , on
trouve :
, on
trouve :
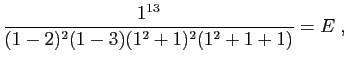
![]()
![]() par
une des racines complexes du trinôme. Dans notre cas, on multiplie
les deux membres par
par
une des racines complexes du trinôme. Dans notre cas, on multiplie
les deux membres par ![]() , et on remplace
, et on remplace ![]() par
par
![]() . On trouve :
. On trouve :
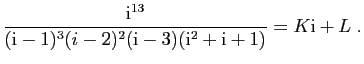
![]() , qui ne soient pas des
racines du dénominateur (
, qui ne soient pas des
racines du dénominateur (![]() ,
, ![]() , etc...).
On peut aussi
penser à faire tendre
, etc...).
On peut aussi
penser à faire tendre ![]() vers l'infini. On n'a recours à une
réduction au même dénominateur avec identification des
coefficients qu'en dernier ressort.
vers l'infini. On n'a recours à une
réduction au même dénominateur avec identification des
coefficients qu'en dernier ressort.
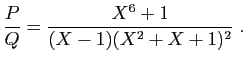
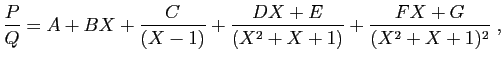
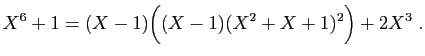
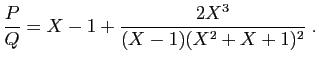
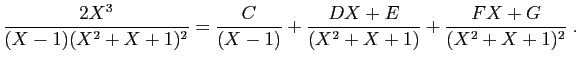
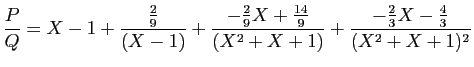
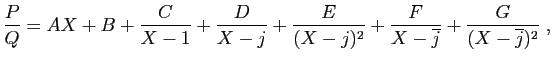
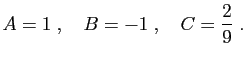
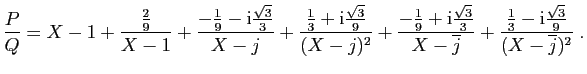
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales