Nous allons utiliser la notion
de bijection pour définir le cardinal d'un ensemble fini.
Intuitivement, deux ensembles ont le même nombre d'éléments
si et seulement si on peut définir une bijection entre
ces ensembles. Les définitions qui suivent formalisent cette
intuition.
Proposition 4
Soient 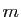 et
et 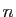 des entiers. S'il existe une injection
des entiers. S'il existe une injection
alors
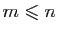 .
.
Démonstration : On raisonne par récurrence sur 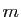 .
Si
.
Si 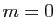 , la conclusion est vérifiée.
Supposons le résultat vrai pour
, la conclusion est vérifiée.
Supposons le résultat vrai pour 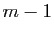 .
Soit
.
Soit
une application injective.
Comme 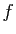 est injective, on a
est injective, on a
On peut donc définir
L'application ainsi définie est injective. Donc, par
hypothèse de récurrence,
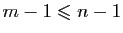 . D'où
. D'où
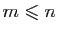 .
.
Corollaire 2
Soient 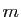 et
et 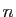 des entiers.
S'il existe une bijection de
des entiers.
S'il existe une bijection de
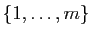 sur
sur
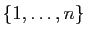 ,
alors
,
alors 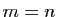 .
.
Démonstration : Notons 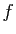 une telle bijection. Alors
une telle bijection. Alors 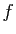 et
et 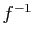 sont
injectives et on applique la proposition précédente.
sont
injectives et on applique la proposition précédente.
Ce corollaire montre que si  est un ensemble de cardinal
est un ensemble de cardinal 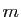 et
de cardinal
et
de cardinal 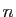 , alors
, alors 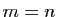 . En effet, dans ce cas il existe
une bijection
. En effet, dans ce cas il existe
une bijection 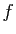 de
de  sur
sur
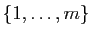 et
et 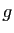 de
de  sur
sur
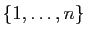 et
et
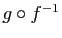 fournit une bijection de
fournit une bijection de
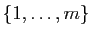 sur
sur
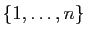 .
.
Définition 6
Soit  un ensemble fini. On appelle cardinal de
un ensemble fini. On appelle cardinal de  et
on note
et
on note
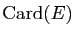 l'unique entier
l'unique entier 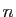 tel que
tel que  soit
de cardinal
soit
de cardinal 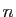 .
.
Exemple 1
Si 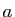 ,
,
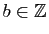 , avec
, avec
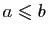 , alors
, alors
En effet l'application
est bijective.
Proposition 5
Soit  un ensemble fini et
un ensemble fini et 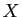 une partie de
une partie de  . Alors
. Alors
- L'ensemble
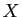 est fini;
est fini;
-
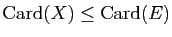 ;
;
- Si
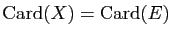 , alors
, alors 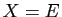 .
.
Démonstration : Soit 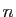 le cardinal de
le cardinal de  . Il existe donc une bijection
. Il existe donc une bijection 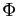 de
de  sur
sur
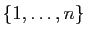 . L'application
obtenue par restriction à
. L'application
obtenue par restriction à 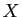 :
:
est également bijective. Quitte à remplacer 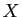 par
par
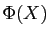 , il suffit de traiter le cas où
, il suffit de traiter le cas où
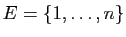 .
.
On raisonne alors par récurrence sur le cardinal de  .
Si
.
Si 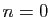 , alors
, alors
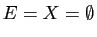 et le résultat est valide.
Supposons le résultat démontré pour les ensembles
de cardinal
et le résultat est valide.
Supposons le résultat démontré pour les ensembles
de cardinal 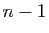 , et montrons le pour
, et montrons le pour
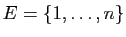 .
Si
.
Si 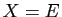 , alors
, alors
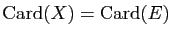 et
les assertions a), b) et c)
sont vérifiées.
Si
et
les assertions a), b) et c)
sont vérifiées.
Si 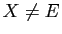 , il nous suffit de montrer que
, il nous suffit de montrer que 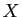 est fini
de cardinal inférieur ou égal à
est fini
de cardinal inférieur ou égal à 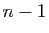 .
Mais dans ce cas, il existe
.
Mais dans ce cas, il existe
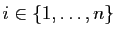 tel que
tel que
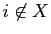 .
On considère alors l'application
.
On considère alors l'application
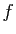 est bijective, donc
est bijective, donc
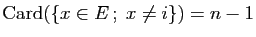 et par hypothèse de récurrence
et par hypothèse de récurrence 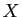 est fini et
est fini et
ce qui montre les assertions dans ce cas.
Démonstration : Si 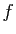 est injective,
on considère l'application
est injective,
on considère l'application
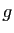 est bijective. Donc
est bijective. Donc  et
et 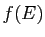 ont même cardinal.
Donc
ont même cardinal.
Donc
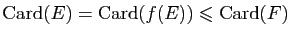 . L'application
. L'application 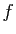 est
bijective si et seulement si
est
bijective si et seulement si 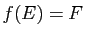 ce qui est équivalent à
ce qui est équivalent à
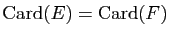 par ce qui précède.
par ce qui précède.
Supposons 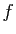 surjective, c'est-à-dire telle
que
surjective, c'est-à-dire telle
que
Donc il existe une application 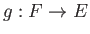 telle
que
telle
que
La composée 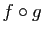 est l'application identique de
est l'application identique de 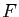 ,
donc
,
donc 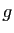 est injective.
On applique alors le cas injectif à
est injective.
On applique alors le cas injectif à 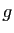 .
.
Rappelons la définition du complémentaire. Soient  et
et 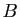 deux
ensembles. On note
deux
ensembles. On note
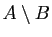 l'ensemble des élements de
l'ensemble des élements de  qui
n'appartiennent pas à
qui
n'appartiennent pas à 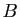 .
.
Si
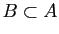 ,
,
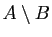 est appelé
le complémentaire de
est appelé
le complémentaire de 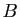 dans
dans  .
.
Proposition 6
Si  est fini et
est fini et
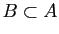 , alors
, alors
Démonstration : Par la proposition 5, on sait que 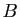 et
et
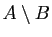 sont finis. Notons
sont finis. Notons 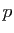 le cardinal de
le cardinal de 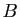 et
et 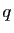 le cardinal de
le cardinal de
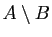 .
Il existe donc des bijections
.
Il existe donc des bijections
et
L'application
est bijective donc
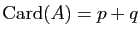 .
.
Démonstration : On raisonne par récurrence sur 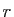 .
.
Si  ,
, 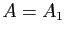 et le résultat est vrai.
Si c'est vrai pour
et le résultat est vrai.
Si c'est vrai pour 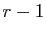 , par hypothèse de récurrence,
appliquée à l'ensemble
, par hypothèse de récurrence,
appliquée à l'ensemble
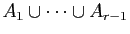 ,
on a
,
on a
Mais
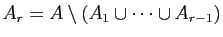 .
Donc
.
Donc
ce qui prouve le résultat pour 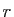 .
.
Exemple 2
Ainsi
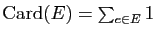 .
.
On peut définir de même le produit
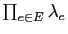 .
.
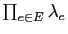
Corollaire 4 (Principe des bergers)
Soient  un ensemble fini et
un ensemble fini et 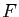 un ensemble. Soit
un ensemble. Soit 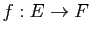 une application, alors
une application, alors 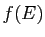 est fini et :
est fini et :
Démonstration : L'application
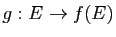 définie par
définie par 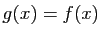 pour tout
pour tout 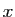 de
de  est surjective. Par conséquent,
est surjective. Par conséquent, 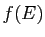 est fini.
Soit
est fini.
Soit
 . On fixe donc une bijection
. On fixe donc une bijection
On applique alors la proposition à la famille
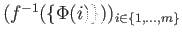 de parties de
de parties de  .
.
Proposition 8
Soient  et
et 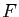 des ensembles finis, alors :
des ensembles finis, alors :
-
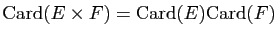 ;
;
-
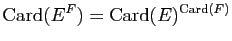 ;
;
-
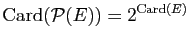 .
.
Démonstration : Pour a), on considère l'application surjective
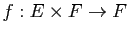 qui applique
qui applique 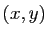 sur
sur 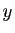 et on applique la proposition précédente, en notant
que pour tout
et on applique la proposition précédente, en notant
que pour tout 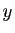 de
de 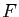 , l'application
, l'application
est bijective.
Pour b), on raisonne par récurrence sur
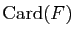 en considérant
pour tout
en considérant
pour tout 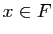 l'application
l'application
Pour c), on vérifie que l'application
de
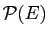 sur
sur 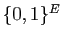 qui envoie une partie
qui envoie une partie
 sur l'application
sur l'application
est bijective.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() un ensemble et
un ensemble et ![]() un entier. On dit que
un entier. On dit que ![]() est
de cardinal
est
de cardinal ![]() si
si ![]() et
et
![]() ont le
même cardinal.
ont le
même cardinal.
![]() un ensemble. On dit que
un ensemble. On dit que ![]() est fini
s'il existe un entier
est fini
s'il existe un entier ![]() tel que
tel que ![]() soit de cardinal
soit de cardinal ![]() .
.
![]() un ensemble et
un ensemble et ![]() un entier. On dit que
un entier. On dit que ![]() est
de cardinal
est
de cardinal ![]() si
si ![]() et
et
![]() ont le
même cardinal.
ont le
même cardinal.
![]() un ensemble. On dit que
un ensemble. On dit que ![]() est fini
s'il existe un entier
est fini
s'il existe un entier ![]() tel que
tel que ![]() soit de cardinal
soit de cardinal ![]() .
.
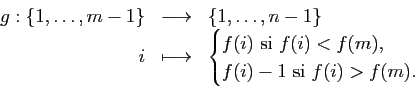
![]() est un ensemble de cardinal
est un ensemble de cardinal ![]() et
de cardinal
et
de cardinal ![]() , alors
, alors ![]() . En effet, dans ce cas il existe
une bijection
. En effet, dans ce cas il existe
une bijection ![]() de
de ![]() sur
sur
![]() et
et ![]() de
de ![]() sur
sur
![]() et
et
![]() fournit une bijection de
fournit une bijection de
![]() sur
sur
![]() .
.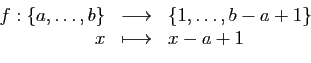
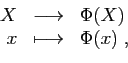
![]() .
Si
.
Si ![]() , alors
, alors
![]() et le résultat est valide.
Supposons le résultat démontré pour les ensembles
de cardinal
et le résultat est valide.
Supposons le résultat démontré pour les ensembles
de cardinal ![]() , et montrons le pour
, et montrons le pour
![]() .
Si
.
Si ![]() , alors
, alors
![]() et
les assertions a), b) et c)
sont vérifiées.
Si
et
les assertions a), b) et c)
sont vérifiées.
Si ![]() , il nous suffit de montrer que
, il nous suffit de montrer que ![]() est fini
de cardinal inférieur ou égal à
est fini
de cardinal inférieur ou égal à ![]() .
Mais dans ce cas, il existe
.
Mais dans ce cas, il existe
![]() tel que
tel que
![]() .
On considère alors l'application
.
On considère alors l'application
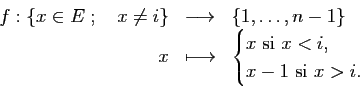
![]() est fini et si
est fini et si ![]() est injective,
alors
est injective,
alors
![]() est fini et si
est fini et si ![]() est surjective,
alors
est surjective,
alors
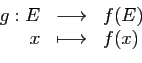
![]() surjective, c'est-à-dire telle
que
surjective, c'est-à-dire telle
que
![]() et
et ![]() deux
ensembles. On note
deux
ensembles. On note
![]() l'ensemble des élements de
l'ensemble des élements de ![]() qui
n'appartiennent pas à
qui
n'appartiennent pas à ![]() .
.
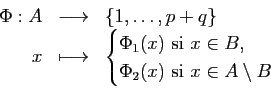
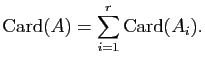
![]() ,
, ![]() et le résultat est vrai.
Si c'est vrai pour
et le résultat est vrai.
Si c'est vrai pour ![]() , par hypothèse de récurrence,
appliquée à l'ensemble
, par hypothèse de récurrence,
appliquée à l'ensemble
![]() ,
on a
,
on a
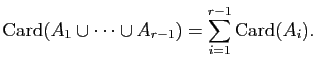
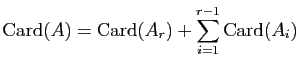
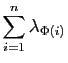
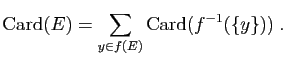
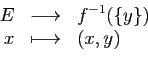
![]() en considérant
pour tout
en considérant
pour tout ![]() l'application
l'application
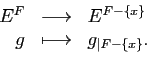
![]() sur
sur ![]() qui envoie une partie
qui envoie une partie
![]() sur l'application
sur l'application
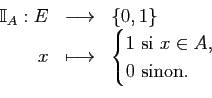
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales