... n'existe pas ! Un ensemble 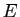 n'est
défini que si pour tout objet
n'est
défini que si pour tout objet 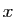 l'énoncé
l'énoncé
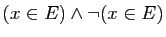 est faux.
est faux.
Démonstration : C'est un exemple de démonstration par l'absurde. Supposons que
l'ensemble de tous les ensembles existe, et notons-le 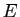 . Notons
. Notons  l'ensemble
l'ensemble
Comme 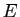 contient tous les ensembles,
contient tous les ensembles,  appartient à
appartient à 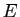 .
Est-ce que
.
Est-ce que  appartient à
appartient à  ?
?

- si
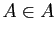 alors par définition de
alors par définition de  ,
, 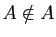 ,
,

- si
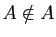 alors par définition de
alors par définition de  ,
, 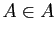 .
.
L'assertion 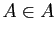 ne peut pas être vraie et fausse en même
temps, c'est donc que l'hypothèse de départ (
ne peut pas être vraie et fausse en même
temps, c'est donc que l'hypothèse de départ (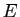 existe) était
fausse.
existe) était
fausse.
Des versions plus prosaïques de ce paradoxe sont connues depuis
l'antiquité. Par exemple :
Epiménide le Crétois a dit : tous les Crétois sont des menteurs
ou bien
Le barbier rase tous ceux qui ne se rasent pas eux-mêmes.
D'autres notions, apparemment claires, ne sont pas définies parce
qu'elles conduisent à une contradiction. Par exemple :
Le plus petit nombre qu'on ne puisse pas
définir en moins de vingt mots
(la phrase ci-dessus comporte quinze mots).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales