Une projection qui est moins utilisée par les géographes, mais qui présente de remarquables propriétés mathématiques, est la projection stéréographique.
On projette la surface de la terre, assimilée à la sphère unité, sur le plan de l'équateur par une projection centrale de centre le pôle Nord. Par tout point ![]() de la terre distinct du pôle Nord
de la terre distinct du pôle Nord ![]() , on trace donc la droite
, on trace donc la droite ![]() , qui coupe le plan de l'équateur en un unique point
, qui coupe le plan de l'équateur en un unique point ![]() .
.
![\includegraphics[width=0.7\textwidth]{stereo}](img1502.gif)
Si on rapporte l'espace à un repère orthonormé d'origine le centre ![]() de la sphère et tel que
de la sphère et tel que ![]() ait pour coordonnées
ait pour coordonnées ![]() , cette transformation
, cette transformation ![]() est donnée en formules par
est donnée en formules par
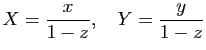
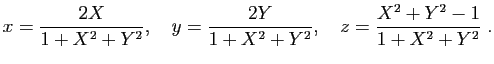
Ces formules permettent de montrer que l'image par ![]() de tout cercle tracé sur la sphère est une droite ou un cercle : plus précisément, c'est une droite si le cercle passe par
de tout cercle tracé sur la sphère est une droite ou un cercle : plus précisément, c'est une droite si le cercle passe par ![]() et un cercle sinon.
et un cercle sinon.
Si on identifie le plan ![]() au corps des nombres complexes en associant à chaque point son affixe, on obtient ainsi une bijection de la sphère privée du point
au corps des nombres complexes en associant à chaque point son affixe, on obtient ainsi une bijection de la sphère privée du point ![]() sur
sur
![]() . Pour obtenir une bijection définie sur la sphère tout entière, on complète
. Pour obtenir une bijection définie sur la sphère tout entière, on complète
![]() par un point à l'infini : en effet, quand un point
par un point à l'infini : en effet, quand un point ![]() de la sphère s'approche de
de la sphère s'approche de ![]() , son image
, son image ![]() s'éloigne à l'infini.
s'éloigne à l'infini.
Le plan complexe ainsi complété, noté
![]() , est appelé sphère de Riemann et constitue le cadre naturel pour étudier les homographies.
, est appelé sphère de Riemann et constitue le cadre naturel pour étudier les homographies.
Une homographie est une application
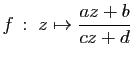 où
où ![]() sont des nombres complexes vérifiant
sont des nombres complexes vérifiant
![]() (sinon l'application serait constante). Cette application définit, si
(sinon l'application serait constante). Cette application définit, si ![]() , une bijection de
, une bijection de
![]() privé du point
privé du point ![]() sur
sur
![]() privé du point
privé du point ![]() (si
(si ![]() , c'est une similitude directe). On la complète en une bijection de
, c'est une similitude directe). On la complète en une bijection de
![]() sur
sur
![]() en posant
en posant
![]() et
et
![]() . Elle a la propriété de transformer une droite ou un cercle en une droite ou un cercle.
. Elle a la propriété de transformer une droite ou un cercle en une droite ou un cercle.
Projection stéréographique et projection de Mercator
Si on repère le point ![]() de la sphère par sa latitude
de la sphère par sa latitude ![]() et sa longitude
et sa longitude ![]() et son projeté
et son projeté ![]() sur le plan
sur le plan ![]() par ses coordonnées polaires
par ses coordonnées polaires ![]() et
et ![]() , on voit sur la figure dans le plan
, on voit sur la figure dans le plan ![]() que
que
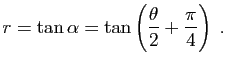
![\includegraphics[width=8cm]{stereoggb}](img1522.gif)
L'affixe du point ![]() est donc
est donc
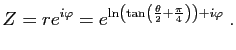
Pour en savoir plus sur la projection stéréographique et sur d'autres sujets abordés dans ces compléments (et sur bien d'autres choses encore), vous pouvez consulter le site : http://www.dimensions-math.org/Dim_fr.htm qui vous fera voyager jusque dans la quatrième dimension.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales