L'objet de cette section est de donner des conditions sur un ouvert
de
![]() qui permettent d'assurer l'existence de primitives pour les
fonctions continues définies sur cet ouvert.
qui permettent d'assurer l'existence de primitives pour les
fonctions continues définies sur cet ouvert.
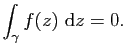
Démonstration : La nécessité de la condition a été prouvée dans le premier exemple de la section 1.2.
Supposons la condition satisfaite, nous devons construire une
primitive ![]() de
de ![]() sur chaque composante connexe de
sur chaque composante connexe de ![]() . Sans
perte de généralité nous pouvons supposer que
. Sans
perte de généralité nous pouvons supposer que ![]() est connexe. Pour
tout couple de points
est connexe. Pour
tout couple de points ![]() ,
, ![]() de
de ![]() , il existe donc un chemin de
classe
, il existe donc un chemin de
classe
![]() contenu dans
contenu dans ![]() joignant
joignant ![]() à
à ![]() . Si
. Si
![]() est un tel chemin, on définit le chemin
est un tel chemin, on définit le chemin
![]() par
par
![]() et on a
et on a
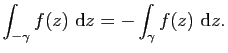
Montrons que
![]() ne dépend pas du choix du
chemin
ne dépend pas du choix du
chemin ![]() contenu dans
contenu dans ![]() joignant
joignant ![]() à
à ![]() . Si
. Si ![]() et
et ![]() sont deux chemins de classe
sont deux chemins de classe
![]() contenus dans
contenus dans ![]() joignant
joignant ![]() à
à ![]() . Notons
. Notons ![]() le chemin obtenu en
juxtaposant le chemin
le chemin obtenu en
juxtaposant le chemin ![]() et le chemin
et le chemin ![]() , c'est un
chemin fermé de classe
, c'est un
chemin fermé de classe
![]() par morceaux dans
par morceaux dans ![]() (figure 5).
(figure 5).
Par hypothèse on a donc
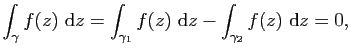
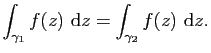
Fixons ![]() , on peut alors définir pour
, on peut alors définir pour ![]()
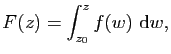
Il reste à prouver que ![]() est une primitive de
est une primitive de ![]() sur
sur ![]() . Pour
. Pour
![]() assez petit pour que le segment
assez petit pour que le segment ![]() d'extrémités
d'extrémités
![]() et
et ![]() soit contenu dans
soit contenu dans ![]() on a
on a
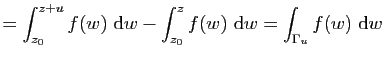 |
||
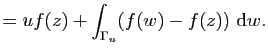 |
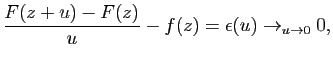
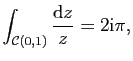
Exemple. Un ouvert convexe ![]() est étoilé par
rapport à chacun de ses points.
est étoilé par
rapport à chacun de ses points.
Si ![]() est un triangle fermé de
est un triangle fermé de
![]() , on désigne par
, on désigne par
![]() le chemin de classe
le chemin de classe
![]() par morceaux constitué du
bord du triangle
par morceaux constitué du
bord du triangle ![]() parcouru une fois dans le sens direct.
parcouru une fois dans le sens direct.
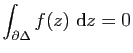
![$\displaystyle F(z)=\int_{[z_0,z]}f(w) \mathrm{d}w.$](img468.gif)
![$\displaystyle F(z+u)-F(z)=\int_{[z,z+u]}f(w) \mathrm{d}w$](img473.gif)
Résumé. Soit ![]() est une fonction continue
dans un ouvert
est une fonction continue
dans un ouvert ![]() de
de
![]() .
.
|
||||||
|
|
|
|||||
|
|
|
||||
Théorèmes de Cauchy
Nous développons ici la théorie de Cauchy pour les domaines convexes ou étoilés.
Démonstration : Nous utilisons la méthode de Goursat. Soient
Posons
![]() . La valeur absolue d'une au moins des quatre intégrales
. La valeur absolue d'une au moins des quatre intégrales
![]() est supérieure ou égale à
est supérieure ou égale à
![]() . Soit
. Soit ![]() le triangle correspondant à une
telle intégrale. En appliquant à
le triangle correspondant à une
telle intégrale. En appliquant à ![]() le raisonnement fait
pour
le raisonnement fait
pour ![]() , on construit un triangle
, on construit un triangle ![]() tel que
tel que
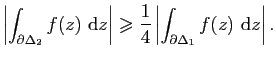
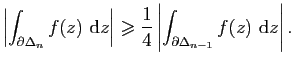
La famille
![]() est une suite décroissante de
compacts dont le diamètre tend vers 0, donc
est une suite décroissante de
compacts dont le diamètre tend vers 0, donc
![]() . En effet
. En effet
![]() car sinon il existerait une
sous famille finie d'intersection vide, ce qui contredirait la
décroissance de la famille; elle est réduite à un point car le
diamètre des
car sinon il existerait une
sous famille finie d'intersection vide, ce qui contredirait la
décroissance de la famille; elle est réduite à un point car le
diamètre des ![]() tend vers 0.
tend vers 0.
Comme
![]() ,
, ![]() est
est
![]() -dérivable en
-dérivable en ![]() par
hypothèse. Par conséquent
par
hypothèse. Par conséquent
![]() étant donné, il existe
étant donné, il existe
![]() tel que pour
tel que pour
![]() on ait
on ait
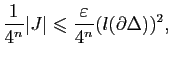
Remarque. Le résultat du théorème précédent reste vrai si on suppose que ![]() est continue dans
est continue dans ![]() et
et
![]() -dérivable dans
-dérivable dans ![]() privé d'un point
privé d'un point
![]() .
.
Démonstration : [de la remarque]
Il n'y a à traiter que le cas où
![]() , l'autre cas
résultant directement du Théorème 12.
, l'autre cas
résultant directement du Théorème 12.
Si ![]() est un sommet de
est un sommet de ![]() , par exemple
, par exemple ![]() .
D'après le Théorème 12, si
.
D'après le Théorème 12, si
![]() et
et
![]() ,
,
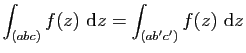
Si ![]() est sur un côté de
est sur un côté de ![]() , on se ramène au cas
précédent en décomposant
, on se ramène au cas
précédent en décomposant ![]() en deux triangles en joignant
en deux triangles en joignant
![]() au sommet opposé. De même si
au sommet opposé. De même si ![]() est à l'intérieur de
est à l'intérieur de
![]() , on décompose
, on décompose ![]() en trois triangles en joignant
en trois triangles en joignant
![]() à chacun des sommets de
à chacun des sommets de ![]() (figure 8).
(figure 8).
Cette extension nous sera utile ultérieurement. Mais en fait elle
n'est qu'apparente car on verra que si ![]() est continue sur
est continue sur ![]() et
et
![]() -dérivable dans
-dérivable dans ![]() privé d'un point elle est
privé d'un point elle est
![]() -dérivable
dans
-dérivable
dans ![]() .
.
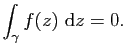
 |
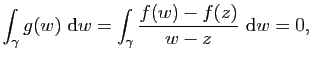
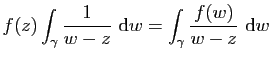
1) La fonction ![]() est
est
![]() -dérivable dans
-dérivable dans ![]()
2) La fonction ![]() est holomorphe dans
est holomorphe dans ![]()
3) La fonction ![]() est analytique dans
est analytique dans ![]()
4) La fonction ![]() admet localement une primitive dans
admet localement une primitive dans ![]()
5) Pour tout triangle ![]() contenu dans
contenu dans ![]() , on a
, on a
![]() .
.
Résumé. Soit ![]() est une fonction continue
dans un ouvert
est une fonction continue
dans un ouvert ![]() de
de
![]() .
.
|
|
|
||||
|
|
||||||
|
|
|
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales