L'étude des projections et symétries, sera l'occasion de mettre en
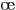 uvre à la fois des applications linéaires entre espaces
vectoriels généraux et les sommes d'espaces vectoriels.
Aussi bien pour les projections que pour les symétries,
l'ingrédient principal est une somme directe. Soit
uvre à la fois des applications linéaires entre espaces
vectoriels généraux et les sommes d'espaces vectoriels.
Aussi bien pour les projections que pour les symétries,
l'ingrédient principal est une somme directe. Soit 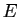 un espace
vectoriel,
un espace
vectoriel,  et
et 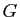 deux sous-espaces tels que
deux sous-espaces tels que
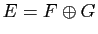 . Pour
tout vecteur
. Pour
tout vecteur 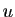 dans
dans 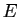 , il existe un couple unique de vecteurs
, il existe un couple unique de vecteurs
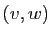 tels que
tels que 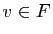 ,
, 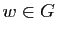 et
et 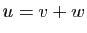 (voir la proposition
4 et la figure 1).
(voir la proposition
4 et la figure 1).
Définition 11
Soit 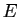 un espace vectoriel,
un espace vectoriel,  et
et 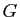 deux sous-espaces tels que
deux sous-espaces tels que
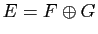 .
.
- On appelle projection sur
 parallèlement à
parallèlement à 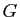 l'application qui à
l'application qui à 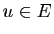 associe l'unique élément
associe l'unique élément 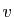 de
de  tel que
tel que 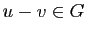 .
.
- On appelle symétrie par rapport à
 parallèlement à
parallèlement à 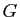 l'application qui à
l'application qui à 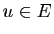 associe
associe 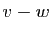 , où
, où 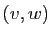 est le
couple unique de vecteurs
tels que
est le
couple unique de vecteurs
tels que 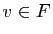 ,
, 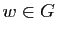 et
et 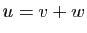 .
.
La figure 2 illustre la projection sur  parallèlement à
parallèlement à 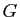 et la
symétrie correspondante. Reprenons par exemple la décomposition de
l'espace des polynômes
et la
symétrie correspondante. Reprenons par exemple la décomposition de
l'espace des polynômes
![$ \mathbb{R}[X]=F\oplus G$](img349.gif) , où
, où  (respectivement : G) est l'ensemble
des polynômes ne contenant que des termes de degré pair
(respectivement : impair).
La projection
(respectivement : G) est l'ensemble
des polynômes ne contenant que des termes de degré pair
(respectivement : impair).
La projection 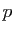 sur
sur  parallèlement à
parallèlement à 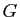 associe à un polynôme, le polynôme formé par ses termes de
degré pair.
associe à un polynôme, le polynôme formé par ses termes de
degré pair.
La symétrie par rapport à  change le signe des termes de
degré impair (transformation
change le signe des termes de
degré impair (transformation
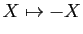 ).
).
Figure 2:
Somme directe
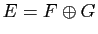 , projection sur
, projection sur  ,
et symétrie par rapport à
,
et symétrie par rapport à  .
.
|
|
Proposition 10
Soit 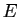 un espace vectoriel,
un espace vectoriel,  et
et 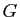 deux sous-espaces tels que
deux sous-espaces tels que
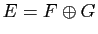 . La projection sur
. La projection sur  d'une part, et
la symétrie par rapport à
d'une part, et
la symétrie par rapport à  parallèlement à
parallèlement à 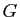 d'autre part,
sont des
applications linéaires.
d'autre part,
sont des
applications linéaires.
Démonstration : Si 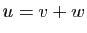 et
et 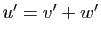 , alors
, alors
Puisque les vecteurs
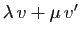 et
et
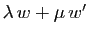 appartiennent respectivement à
appartiennent respectivement à  et
et  ,
la formule précédente donne la décomposition de
,
la formule précédente donne la décomposition de
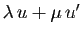 . Sa projection sur
. Sa projection sur  est donc
est donc
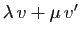 , et son symétrique par rapport à
, et son symétrique par rapport à  est
est
d'où le résultat. La projection sur
La projection sur  parallèlement à
parallèlement à 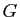 a pour image
a pour image  et pour
noyau
et pour
noyau 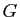 . La symétrie est une bijection de
. La symétrie est une bijection de 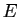 sur lui-même :
c'est un automorphisme de
sur lui-même :
c'est un automorphisme de 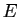 .
La proposition
suivante caractérise les projections et les symétries,
indépendamment de la décomposition en somme directe.
.
La proposition
suivante caractérise les projections et les symétries,
indépendamment de la décomposition en somme directe.
Proposition 11
Soit 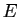 un espace vectoriel.
un espace vectoriel.
- Un endomorphisme
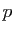 de
de 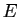 est une projection si et seulement si
est une projection si et seulement si
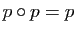 .
.
- Un endomorphisme
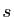 de
de 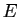 est une symétrie si et seulement si
est une symétrie si et seulement si
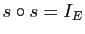 , où
, où 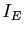 désigne l'application identique de
désigne l'application identique de 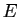 .
.
Démonstration : Si 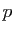 est la projection sur
est la projection sur  parallèlement à
parallèlement à 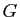 , alors pour
tout
, alors pour
tout 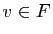 ,
, 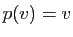 , et donc
, et donc
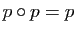 . Réciproquement, si
. Réciproquement, si
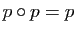 , nous allons montrer que
, nous allons montrer que 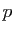 est la projection sur
Im
est la projection sur
Im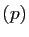 parallèlement à
Ker
parallèlement à
Ker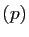 . Commençons par
montrer que
Im
. Commençons par
montrer que
Im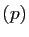 et
Ker
et
Ker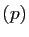 sont supplémentaires,
c'est-à-dire que
sont supplémentaires,
c'est-à-dire que
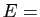 Im
Im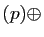 Ker
Ker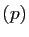 . Observons que
pour tout
. Observons que
pour tout 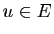 ,
,
donc
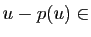 Ker
Ker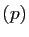 . On peut toujours écrire
. On peut toujours écrire
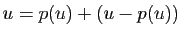 . Pour vérifier que la somme est directe, nous devons
montrer que l'intersection de l'image et du noyau est réduite au
vecteur nul. Si
. Pour vérifier que la somme est directe, nous devons
montrer que l'intersection de l'image et du noyau est réduite au
vecteur nul. Si
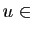 Im
Im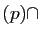 Ker
Ker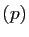 , alors il
existe
, alors il
existe 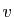 tel que
tel que 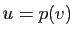 (puisque
(puisque 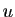 est dans l'image), et de plus
est dans l'image), et de plus
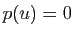 (puisque
(puisque 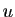 est dans le noyau). Donc
est dans le noyau). Donc 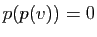 . Mais
. Mais
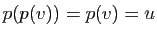 . D'où le résultat.
. D'où le résultat.
Nous avons montré que
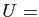 Im
Im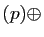 Ker
Ker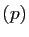 . La
décomposition d'un vecteur
. La
décomposition d'un vecteur 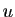 selon cette somme directe est
selon cette somme directe est
Donc 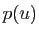 est bien la projection de
est bien la projection de 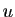 sur
Im
sur
Im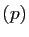 parallèlement à
Ker
parallèlement à
Ker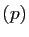 .
La formule
.
La formule
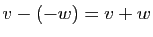 entraîne que la composée
d'une symétrie par elle-même est l'application identique.
Réciproquement, soit
entraîne que la composée
d'une symétrie par elle-même est l'application identique.
Réciproquement, soit 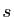 une application telle que
une application telle que
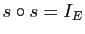 . Définissons les applications
. Définissons les applications 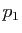 et
et 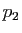 par :
par :
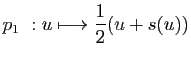
et
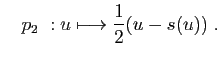
Composons l'application 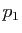 par elle-même :
par elle-même :
On vérifie de même que
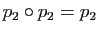 . D'après ce qui
précède,
. D'après ce qui
précède, 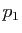 et
et 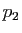 sont donc des projections. Or
sont donc des projections. Or
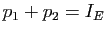 . Il s'ensuit que si
. Il s'ensuit que si 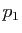 est la projection sur
est la projection sur  parallèlement à
parallèlement à 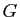 , alors
, alors 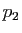 est la projection sur
est la projection sur 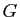 parallèlement à
parallèlement à  . Mais puisque
. Mais puisque 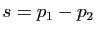 , alors
, alors 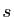 est la
symétrie par rapport à
est la
symétrie par rapport à  , parallèlement à
, parallèlement à 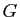 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() Im
Im![]() Ker
Ker![]() . La
décomposition d'un vecteur
. La
décomposition d'un vecteur ![]() selon cette somme directe est
selon cette somme directe est
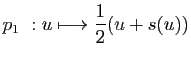 et
et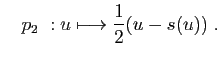
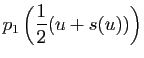
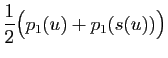
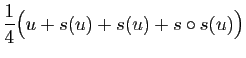
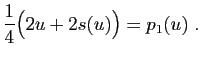
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales