D'autres polynômes, à valeurs complexes, vont nous donner
l'occasion d'évoquer
l'![]() uvre de Joseph Fourier2 (1768 - 1830).
uvre de Joseph Fourier2 (1768 - 1830).
À l'âge de 30 ans, jeune professeur à l'École Polytechnique, il est invité par Bonaparte à participer à l'expédition d'Égypte. Ce voyage déterminera largement le cours de sa vie. D'abord sa carrière : ses qualités d'organisateur et de négociateur, louées par tous là-bas (amis et ennemis), lui vaudront au retour d'être nommé préfet de l'Isère, où il restera de 1802 à 1815. Elles lui vaudront aussi d'être le coordonnateur de la publication du rapport de l'expédition (10 volumes de planches gravées, 9 volumes de texte, et un atlas), dont il rédigera la préface. Fourier n'eut jamais de vie de famille, et aucune liaison sentimentale connue. Ce n'est pas qu'il n'ait jamais eu d'occasion. Dans une lettre3 à un de ses anciens professeurs d'Auxerre devenu son ami, il fait part avec humour de son sentiment sur les accusations portées contre son action pendant la Terreur.
C'est donc de la terreur que j'ai inspirée. Ma foi je ne vois pas que j'en aie fait éprouver aux êtres les plus faibles, aux femmes. Et si j'en avais cru quelques unes, elles me paraissaient fort disposées à d'énormes sacrifices.On ne lui connaît qu'un seul véritable ami, Jacques-Joseph Champollion. Ce dernier avait fait venir à Grenoble son jeune frère Jean-François en 1801 : il est probable que la passion des deux amis pour les antiquités d'Égypte, ait été à l'origine de la vocation de Jean-François, qui découvrira le secret des hiéroglyphes en 1822.
L'expédition d'Égypte a peut-être eu une autre conséquence, qui pour être plus indirecte, n'en est pas moins fondamentale. Fourier aurait contracté en Égypte une fièvre ou un rhumatisme chronique, qui le rendait très sensible au froid. Arago4, parlant de lui vers la fin de sa vie, dit :
Pour se dérober à de légères atteintes rhumatismales, notre confrère se vêtait, dans la saison la plus chaude de l'année, comme ne le sont même pas les voyageurs condamnés à hiverner au milieu des glaces polaires. On me suppose de l'embonpoint, disait-il quelquefois en riant ; soyez assuré qu'il y a beaucoup à rabattre de cette opinion. Si, à l'exemple des momies égyptiennes, on me soumettait, ce dont Dieu me préserve! à l'opération de désemmaillottement, on ne trouverait pour résidu qu'un corps assez fluet. Je pourrais ajouter, en choisissant aussi mon terme de comparaison sur les bords du Nil, que dans les appartements de Fourier, toujours peu spacieux et fortement chauffés, même en été, les courants d'air auxquels on était exposé près des portes, ressemblaient quelquefois à ce terrible Seïmoun, à ce vent brûlant du désert que les caravanes redoutent à l'égal de la peste.Si la relation particulière que Fourier entretenait avec la chaleur est avérée, l'hypothèse d'une fièvre contractée en Égypte n'est pas confirmée par le passage suivant de la lettre qu'il écrivit à son retour.
Je viens enfin, mon cher Bonard, de terminer mon voyage en Égypte, qui ne me laisse que le plus agréable souvenir. Je suis entré il y a quelques jours dans le port de Toulon et je suis d'une santé aussi bonne que je puis le désirer après d'aussi longues fatigues.
Le travail que Fourier a
réalisé sur la diffusion de la chaleur entre 1804 et
1807, se basait entre autres sur
une intuition géniale : toute fonction continue peut être
approchée par des polynômes trigonométriques.
Considérons la famille de fonctions de
![]() dans
dans
![]() :
:
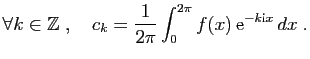
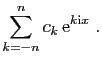
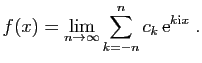
Parce qu'on le soupçonnait de n'avoir pas établi sa méthode sur des bases suffisamment rigoureuses, Fourier a subi de nombreuses critiques en particulier de la part de Poisson. Son travail a été finalement reconnu par une élection à l'Académie des Sciences en 1817, et publié en 1822.
En Égypte, Fourier avait fait l'unanimité par ses qualités humaines. À Grenoble aussi, il était apprécié de tous pour son travail acharné, sa politesse, son sens de la diplomatie et son honnêteté rigoureuse. On dit qu'il était très aimé des Grenoblois et qu'il était même souvent applaudi en ville, par exemple quand il allait au théâtre. Aimé de tous ? Presque !
Une des sources de mon ennui à Grenoble était le petit savant spirituel à l'âme parfaitement petite et à la politesse basse de domestique revêtu, nommé Fourier.Cette citation venimeuse est signée... Stendhal.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales