Avant d'aller plus loin, il convient de préciser ce que nous
entendons par résolution d'une équation
différentielle. Cela recouvre en fait deux
types de problèmes. Le premier est la détermination de l'ensemble
des solutions. La définition suivante précise la notion de
solution pour les équations différentielles d'ordre 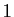 . Elle
s'étend de façon évidente à des équations différentielles
plus générales.
. Elle
s'étend de façon évidente à des équations différentielles
plus générales.
Vous connaissez probablement déjà l'équation 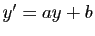 , où
, où 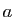 et
et 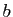 sont deux réels fixés. Vous savez donc que pour tout
intervalle
sont deux réels fixés. Vous savez donc que pour tout
intervalle
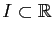 et pour toute constante
et pour toute constante
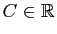 ,
l'application suivante est solution de cette équation sur
,
l'application suivante est solution de cette équation sur  (si
vous ne le savez pas, vérifiez-le en calculant
(si
vous ne le savez pas, vérifiez-le en calculant 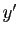 ).
).
Dans cet exemple, il n'y a aucune différence d'expression entre les
solutions définies sur un intervalle 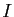 et l'ensemble des solutions
définies sur
et l'ensemble des solutions
définies sur
 .
De façon abrégée, on dira que
.
De façon abrégée, on dira que
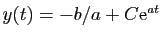 est la
solution générale de l'équation
est la
solution générale de l'équation 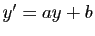 , manière de
dire que l'ensemble des solutions sur
, manière de
dire que l'ensemble des solutions sur
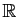 est :
est :
Mais il peut très bien se faire que les solutions ne soient pas
définies sur
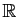 tout entier. C'est le cas bien sûr si
tout entier. C'est le cas bien sûr si 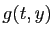 n'est pas défini pour certaines valeurs de
n'est pas défini pour certaines valeurs de 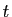 . La définition
1 impose que
. La définition
1 impose que 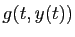 existe pour tout
existe pour tout 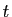 dans l'intervalle
dans l'intervalle 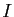 sur lequel
sur lequel 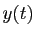 est solution.
Pour en donner des exemples, il
suffit de faire appel aux calculs de primitives, qui sont des
équations différentielles particulières. Considérons par
exemple
est solution.
Pour en donner des exemples, il
suffit de faire appel aux calculs de primitives, qui sont des
équations différentielles particulières. Considérons par
exemple 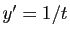 . Il existe des solutions définies sur
. Il existe des solutions définies sur
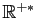 ,
d'autres sur
,
d'autres sur
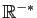 :
:
Il se peut aussi que chaque solution soit définie sur un intervalle
qui lui est propre. Considérons par exemple 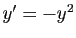 . La seule
solution définie sur
. La seule
solution définie sur
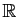 est la fonction nulle. Les autres sont
toutes de la forme suivante.
est la fonction nulle. Les autres sont
toutes de la forme suivante.
Malgré les problèmes de définition, il est
raisonnable de garder en tête l'idée intuitive que la solution
générale d'une équation du premier ordre dépend d'une
constante arbitraire (le réel noté 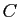 ,
, 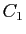 ou
ou 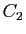 dans les exemples précédents). On peut donc s'attendre à ce
qu'en imposant une condition supplémentaire, on arrive à
déterminer une solution unique.
En général, cette condition
est une valeur fixée de la fonction :
on impose à la solution de passer par un
point donné. Par exemple, vous pouvez vérifier que pour tout
couple
dans les exemples précédents). On peut donc s'attendre à ce
qu'en imposant une condition supplémentaire, on arrive à
déterminer une solution unique.
En général, cette condition
est une valeur fixée de la fonction :
on impose à la solution de passer par un
point donné. Par exemple, vous pouvez vérifier que pour tout
couple
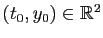 , il existe une solution unique de
l'équation
, il existe une solution unique de
l'équation 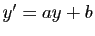 telle que
telle que
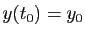 . Ce n'est pas toujours
le cas.
. Ce n'est pas toujours
le cas.
Dans les applications, la variable 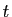 correspond souvent au temps.
Un type de problème fréquent est le calcul d'une
solution partant d'une valeur donnée en
correspond souvent au temps.
Un type de problème fréquent est le calcul d'une
solution partant d'une valeur donnée en 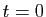 :
cela s'appelle résoudre un problème de Cauchy.
:
cela s'appelle résoudre un problème de Cauchy.
Il existe des théorèmes qui, sous des conditions assez
générales portant sur  , assurent l'existence et l'unicité de
la solution d'un problème de Cauchy. Il peut aussi se faire
qu'il n'y ait aucune solution, ou bien qu'il y en ait une infinité.
Considérons par exemple l'équation
, assurent l'existence et l'unicité de
la solution d'un problème de Cauchy. Il peut aussi se faire
qu'il n'y ait aucune solution, ou bien qu'il y en ait une infinité.
Considérons par exemple l'équation
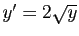 . La fonction
nulle est solution sur
. La fonction
nulle est solution sur
 , et d'autres solutions sont données
par :
, et d'autres solutions sont données
par :
Il se trouve que pour tout
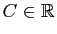 , la fonction définie sur
, la fonction définie sur
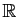 par
par
est solution sur
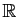 tout entier. Donc le problème de Cauchy
tout entier. Donc le problème de Cauchy
a une infinité de solutions.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
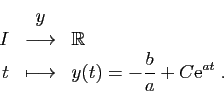
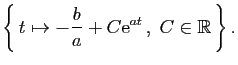
![\begin{displaymath}
\begin{array}{ccl}
&y&\\
]-\infty,0[&\longrightarrow&\mathb...
...rrow&\mathbb{R}\\
t&\longmapsto&y(t)=\ln(t)+C_2\;.
\end{array}\end{displaymath}](img80.gif)
![\begin{displaymath}
\begin{array}{ccl}
&y&\\
]-\infty,C_1[&\longrightarrow&\mat...
...&\longmapsto&y(t)=\displaystyle{\frac{1}{t-C_2}}\;.
\end{array}\end{displaymath}](img82.gif)
![]() correspond souvent au temps.
Un type de problème fréquent est le calcul d'une
solution partant d'une valeur donnée en
correspond souvent au temps.
Un type de problème fréquent est le calcul d'une
solution partant d'une valeur donnée en ![]() :
cela s'appelle résoudre un problème de Cauchy.
:
cela s'appelle résoudre un problème de Cauchy.
![\begin{displaymath}
\begin{array}{ccl}
&y&\\
]C,+\infty[&\longrightarrow&\mathbb{R}\\
t&\longmapsto&y(t)=(t-C)^2\;.
\end{array}\end{displaymath}](img96.gif)
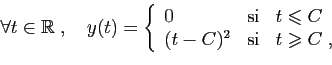
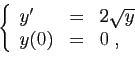
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales