- Calculer les dérivées successives de
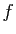 jusqu'à l'ordre
jusqu'à l'ordre
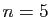 . Écrire le polynôme de Taylor
. Écrire le polynôme de Taylor 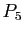 .
.
- Pour
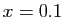 puis
puis 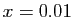 , donner une valeur numérique approchée
de
, donner une valeur numérique approchée
de
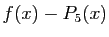 .
.
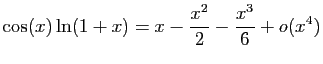 .
.
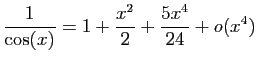 .
.
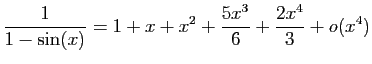 .
.
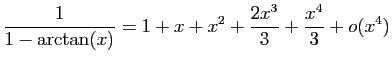 .
.
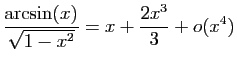 .
.
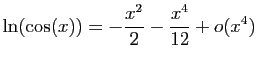 .
.
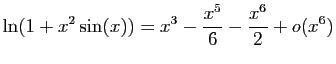 .
.
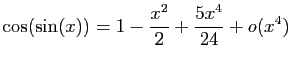 .
.
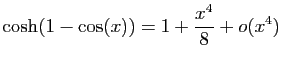 .
.
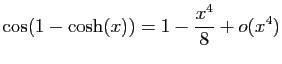 .
.
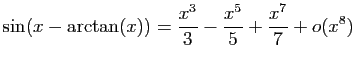 .
.
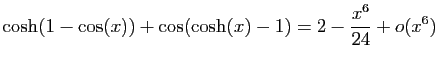 .
.
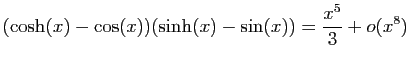 .
.
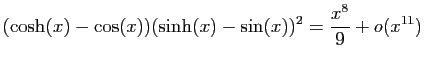 .
.
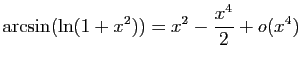 .
.
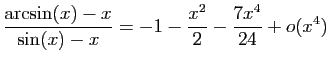 .
.
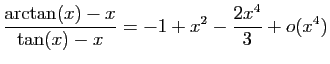 .
.
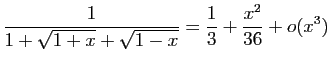 .
.
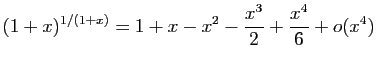 .
.
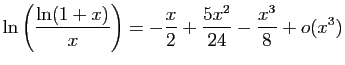 .
.
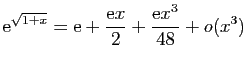 .
.
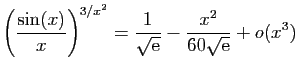 .
.
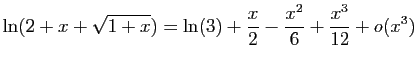 .
.
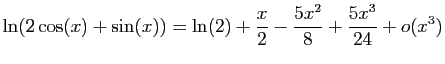 .
.
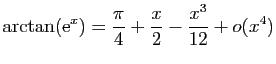 .
.
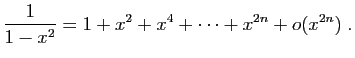
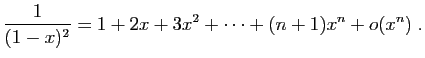
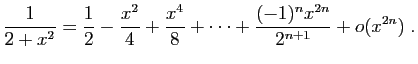
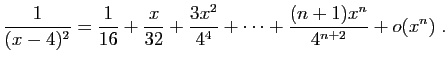


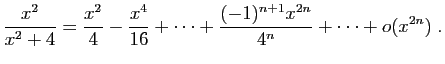
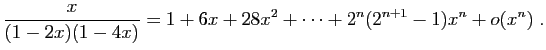
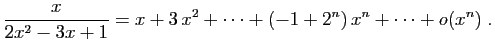
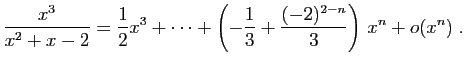
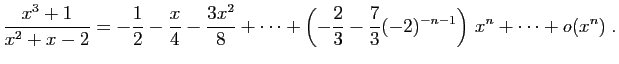
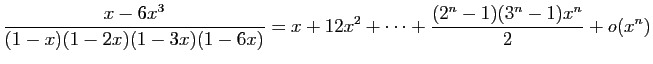 .
.
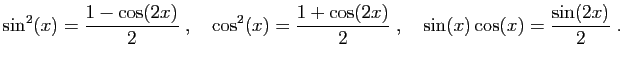
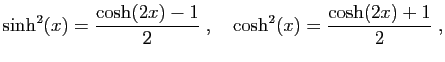
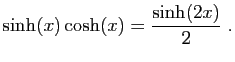
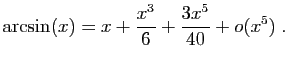
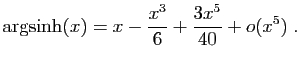
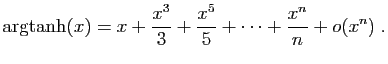
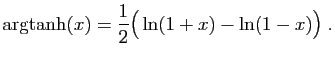
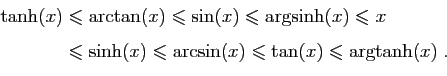
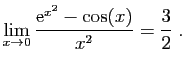
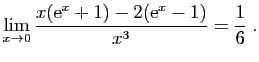
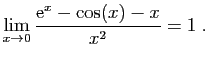
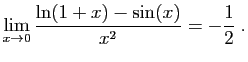
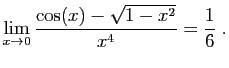
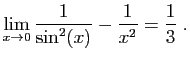
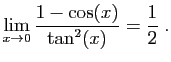
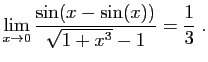
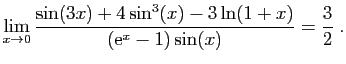
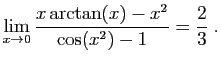
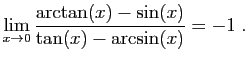
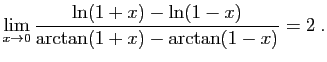
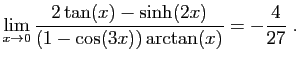
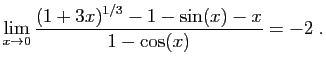
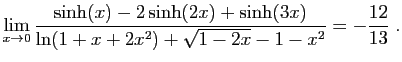
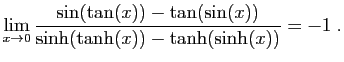
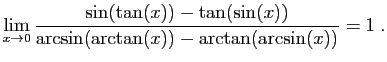
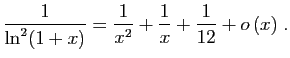
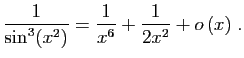
![$ \displaystyle{
\frac{\sqrt{x+x^3}}{\sqrt[3]{x+x^2}}=
x^{1/6}-\frac{x^{7/6}}{3}+\frac{13x^{13/6}}{18}+
o\left(x^{13/6}\right)
}\;.$](img502.gif)
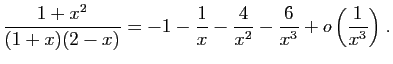
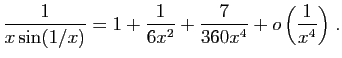
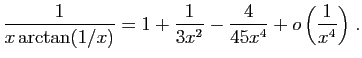
![$ \displaystyle{
\frac{\sqrt{x^3+1}}{\sqrt[3]{x^2+1}}=x^{5/6}
-\frac{1}{3x^{7/6}}+\frac{1}{2x^{13/6}}
+o\left(\frac{1}{x^{13/6}}\right)
}\;.$](img509.gif)
![$ \displaystyle{
\frac{\sqrt{\mathrm{e}^{-x}+\mathrm{e}^{-3x}}}{\sqrt[3]{\mathrm...
...6}}{3}+\frac{13\mathrm{e}^{-13x/6}}{18}+
o\left(\mathrm{e}^{-13x/6}\right)
}\;.$](img510.gif)
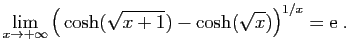
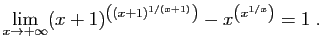
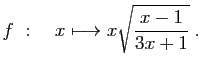
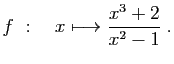
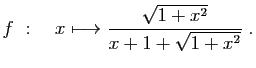
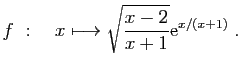
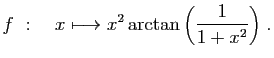
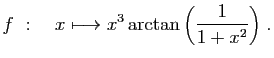
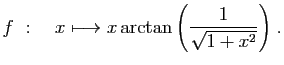
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales