Dans cette partie, on s'intéresse à l'allure locale des courbes planes régulières. Une notion centrale pour connaître cette allure est la courbure. On verra que celle-ci est fortement liée à la dérivée seconde de la paramétrisation.
Rappelons que le déterminant
det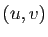 de deux vecteurs
de deux vecteurs
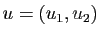 et
et
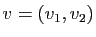 de
de
 est donné par :
est donné par :
det
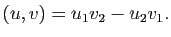
Repère de Serret-Frenet
On définit tout d'abord le repère de Serret-Frenet. Il s'agit d'un repère orthonormé qui varie le long d'une courbe paramétrée.
Le vecteur
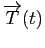 est tangent à la courbe au point
est tangent à la courbe au point 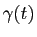 et le vecteur
et le vecteur
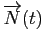 est un vecteur qui est normal à la courbe en
est un vecteur qui est normal à la courbe en 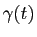 .
.
Remarque : La droite tangente à la courbe 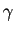 au point
au point 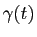 ne dépend pas de la paramétrisation. Par contre, le vecteur
ne dépend pas de la paramétrisation. Par contre, le vecteur
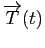 en dépend : si on change le sens de parcours de la courbe, alors ce vecteur sera remplacé par son opposé. Le repère de Serret-Frenet dépend ainsi du sens de parcours de la paramétrisation ainsi que de l'orientation du plan affine.
en dépend : si on change le sens de parcours de la courbe, alors ce vecteur sera remplacé par son opposé. Le repère de Serret-Frenet dépend ainsi du sens de parcours de la paramétrisation ainsi que de l'orientation du plan affine.
Courbure
Quelle est l'allure locale d'une courbe paramétrée
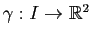 régulière de classe
régulière de classe 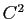 ? On peut supposer, sans restriction, que cette courbe est paramétrée par abscisse curviligne. Pour connaître la forme, on va effectuer un développement limité de
? On peut supposer, sans restriction, que cette courbe est paramétrée par abscisse curviligne. Pour connaître la forme, on va effectuer un développement limité de 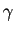 à l'ordre
à l'ordre 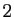 en
en 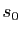 :
:
On sait que le vecteur
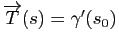 est tangent à la courbe en
est tangent à la courbe en
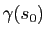 . Si
. Si
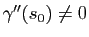 , le développement limité nous indique qu'à l'ordre deux, la courbe est "attirée" dans la direction
, le développement limité nous indique qu'à l'ordre deux, la courbe est "attirée" dans la direction
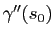 . Autrement dit, le vecteur
. Autrement dit, le vecteur
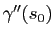 nous donne des informations sur la forme de la courbe au voisinage de
nous donne des informations sur la forme de la courbe au voisinage de
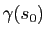 . Intuitivement, on voit aussi que plus
. Intuitivement, on voit aussi que plus
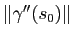 est grand, plus la courbe est courbée. Effectivement, cette norme va nous permettre de définir la courbure (Figure 5).
est grand, plus la courbe est courbée. Effectivement, cette norme va nous permettre de définir la courbure (Figure 5).
Figure 5:
Dérivée première et seconde d'une courbe paramétrée par abscisse curviligne
|
|
Démonstration : Pour tout 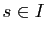 , on a
, on a
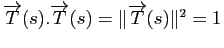 . En dérivant, cela donne
. En dérivant, cela donne
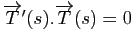 . On pose alors
. On pose alors
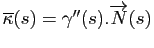 .
. On est maintenant en mesure de définir la courbure d'une courbe paramétrée par abscisse curviligne.
On est maintenant en mesure de définir la courbure d'une courbe paramétrée par abscisse curviligne.
Définition 9
Soit
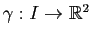 une courbe paramétrée normale régulière de classe
une courbe paramétrée normale régulière de classe 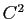 et
et
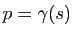 un point de la courbe.
un point de la courbe.
Exemple : Prenons la paramétrisation
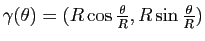 , avec
, avec
![$ \theta \in [0,2\pi ]$](img212.gif) . On remarque que cette paramétrisation est normale car pour tout
. On remarque que cette paramétrisation est normale car pour tout 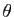 on a
on a
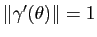 . La courbure au point
. La courbure au point
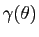 vaut :
vaut :
La courbure d'un cercle de rayon 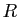 est donc constante et vaut
est donc constante et vaut 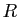 .
.
Démonstration : Admise.
Interprétation géométrique
Si une courbe paramétrée
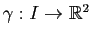 est normale, le point
est normale, le point 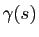 avance à la même vitesse que son paramètre
avance à la même vitesse que son paramètre 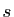 (cela correspond au fait que la norme de la dérivée est constante égale à
(cela correspond au fait que la norme de la dérivée est constante égale à 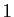 ). Avec cette paramétrisation, on a vu que le vecteur
). Avec cette paramétrisation, on a vu que le vecteur
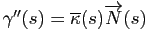 est orthogonal à
est orthogonal à
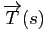 et le développement limité de
et le développement limité de 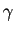 à l'ordre deux peut se réécrire naturellement dans le repère de Serret-Frenet :
à l'ordre deux peut se réécrire naturellement dans le repère de Serret-Frenet :
Figure:
Repère de Serret-Frenet
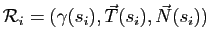 au point de paramètre
au point de paramètre 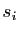 (avec
(avec
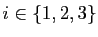 ) : en
) : en
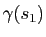 , la courbure algébrique est négative et le vecteur
, la courbure algébrique est négative et le vecteur
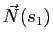 pointe dans la direction opposée au centre de courbure
pointe dans la direction opposée au centre de courbure 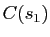 .
En
.
En
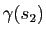 , la courbure algébrique est nulle, il n'y a pas de centre de courbure. En
, la courbure algébrique est nulle, il n'y a pas de centre de courbure. En
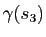 la courbure algébrique est positive et le vecteur
la courbure algébrique est positive et le vecteur
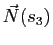 pointe vers le centre de courbure
pointe vers le centre de courbure 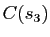 .
.
|
|
En un point de paramètre 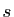 , si la courbure
, si la courbure
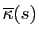 est strictement positive, les vecteurs
est strictement positive, les vecteurs
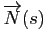 et
et
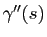 sont égaux et le vecteur
sont égaux et le vecteur
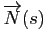 pointe vers le centre de courbure. Si la courbure est négative, alors
pointe vers le centre de courbure. Si la courbure est négative, alors
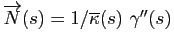 pointe dans la direction opposée au centre de courbure (Figure 6).
pointe dans la direction opposée au centre de courbure (Figure 6).
Proposition 5
Si 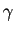 a un point d'inflexion en
a un point d'inflexion en 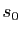 , alors
, alors
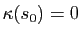 .
.
Démonstration : Il suffit de reprendre le développement limité.
En général, si on prend une courbe paramétrée quelconque, il n'y a pas de raison pour que la paramétrisation soit normale. On peut alors utiliser la proposition suivante pour calculer la courbure :
Proposition 6
Soit
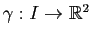 une courbe paramétrée régulière de classe
une courbe paramétrée régulière de classe 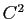 . Alors pour tout
. Alors pour tout 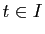 , on a :
, on a :
Démonstration : On note
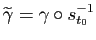 la paramétrisation par abscisse curviligne (avec
la paramétrisation par abscisse curviligne (avec 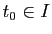 ) et on pose
) et on pose
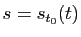 . La formule :
. La formule :
implique
En dérivant une deuxième fois, on a :
où 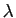 est la dérivée de la fonction
est la dérivée de la fonction
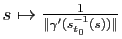 . On a donc :
. On a donc :
det
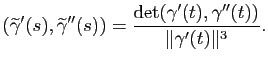
det
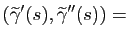
det
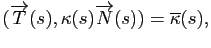

Le cercle de rayon
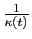 et tangent à la courbe
et tangent à la courbe  au point
au point 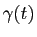 s'appelle le cercle osculateur au point
s'appelle le cercle osculateur au point 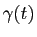 .
.
Sur la Figure 6, on observe que les cercles osculateurs aux points
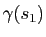 et
et
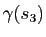 "épousent" bien la forme de la courbe. En fait, ils ont un contact d'ordre deux avec la courbe : plus précisément on peut montrer que la courbe paramétrée par abscisse curviligne et le cercle osculateur paramétré par abscisse curviligne ont un développement limité qui coïncide à l'ordre deux au voisinage du point
"épousent" bien la forme de la courbe. En fait, ils ont un contact d'ordre deux avec la courbe : plus précisément on peut montrer que la courbe paramétrée par abscisse curviligne et le cercle osculateur paramétré par abscisse curviligne ont un développement limité qui coïncide à l'ordre deux au voisinage du point
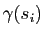 (avec
(avec
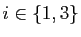 ).
).
Formules de Serret-Frenet
Le repère de Serret Frenet est défini en chaque point d'une courbe paramétrée régulière. Les formules de Serret-Frenet expriment la façon dont ce repère bouge le long de la courbe. Plus précisément, elles donnent les dérivées de ce repère dans la base de Serret-Frenet.
Proposition 7 (Formules de Serret Frenet)
Soit
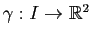 une courbe paramétrée normale régulière de classe
une courbe paramétrée normale régulière de classe 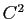 . Alors pour tout
. Alors pour tout 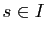 , on a :
, on a :
Démonstration : La première formule a déjà été montrée. Le vecteur
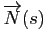 étant unitaire, on a :
étant unitaire, on a :
En dérivant, on obtient
Le vecteur
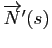 est donc colinéaire à
est donc colinéaire à
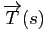 . Par ailleurs, on a :
. Par ailleurs, on a :
En dérivant, on obtient
et donc
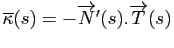 , ce qui permet de conclure.
, ce qui permet de conclure. 
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() au point
au point ![]() ne dépend pas de la paramétrisation. Par contre, le vecteur
ne dépend pas de la paramétrisation. Par contre, le vecteur
![]() en dépend : si on change le sens de parcours de la courbe, alors ce vecteur sera remplacé par son opposé. Le repère de Serret-Frenet dépend ainsi du sens de parcours de la paramétrisation ainsi que de l'orientation du plan affine.
en dépend : si on change le sens de parcours de la courbe, alors ce vecteur sera remplacé par son opposé. Le repère de Serret-Frenet dépend ainsi du sens de parcours de la paramétrisation ainsi que de l'orientation du plan affine.
![]() régulière de classe
régulière de classe ![]() ? On peut supposer, sans restriction, que cette courbe est paramétrée par abscisse curviligne. Pour connaître la forme, on va effectuer un développement limité de
? On peut supposer, sans restriction, que cette courbe est paramétrée par abscisse curviligne. Pour connaître la forme, on va effectuer un développement limité de ![]() à l'ordre
à l'ordre ![]() en
en ![]() :
:
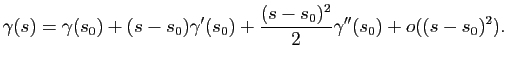
![]() , avec
, avec
![]() . On remarque que cette paramétrisation est normale car pour tout
. On remarque que cette paramétrisation est normale car pour tout ![]() on a
on a
![]() . La courbure au point
. La courbure au point
![]() vaut :
vaut :
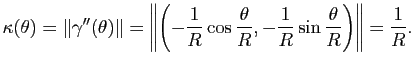
![]() est normale, le point
est normale, le point ![]() avance à la même vitesse que son paramètre
avance à la même vitesse que son paramètre ![]() (cela correspond au fait que la norme de la dérivée est constante égale à
(cela correspond au fait que la norme de la dérivée est constante égale à ![]() ). Avec cette paramétrisation, on a vu que le vecteur
). Avec cette paramétrisation, on a vu que le vecteur
![]() est orthogonal à
est orthogonal à
![]() et le développement limité de
et le développement limité de ![]() à l'ordre deux peut se réécrire naturellement dans le repère de Serret-Frenet :
à l'ordre deux peut se réécrire naturellement dans le repère de Serret-Frenet :
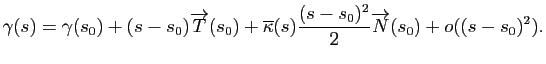
![\includegraphics[height=6cm]{serretfresnet}](img229.gif)
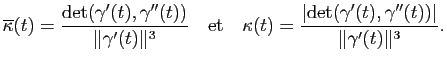
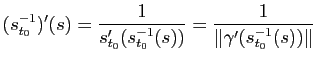
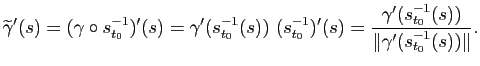
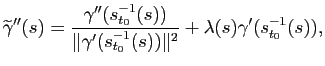
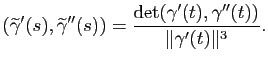
![]() et tangent à la courbe
et tangent à la courbe ![]() au point
au point ![]() s'appelle le cercle osculateur au point
s'appelle le cercle osculateur au point ![]() .
.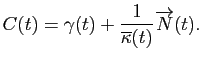
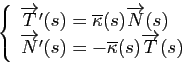
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales