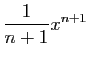 .
.
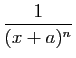 : primitive
: primitive 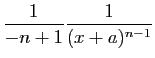 pour
pour 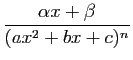 , avec
, avec
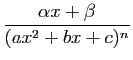 |
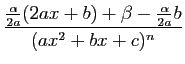 |
||
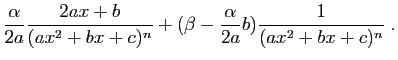 |
![$\displaystyle \int_\gamma^x \frac{2at+b}{(at^2+bt+c)^n} \mathrm{d}t
=
\Big[ \f...
...2+bt+c)^{n-1}}\Big]_\gamma^x
=
\frac{1}{-n+1} \frac{1}{(ax^2+bx+c)^{n-1}}+C\;,
$](img205.gif)
![$\displaystyle \int_\gamma^x \frac{2at+b}{at^2+bt+c} \mathrm{d}t
=
\Big[ \ln\vert at^2+bt+c\vert\Big]_\gamma^x
=
\ln\vert ax^2+bx+c\vert+C\;,
$](img206.gif)
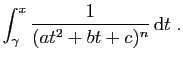
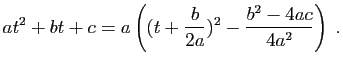
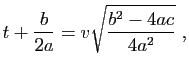
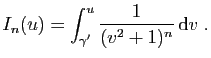
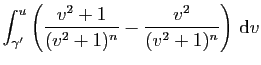 |
|||
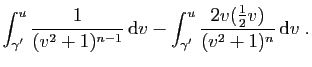 |
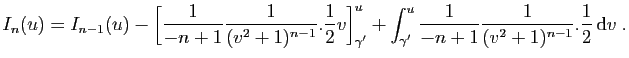
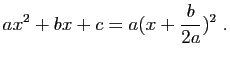
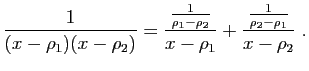
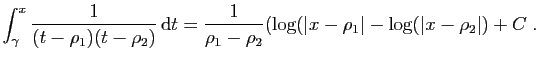
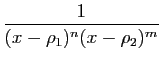 |
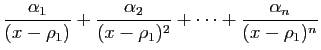 |
||
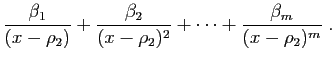 |
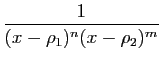 |
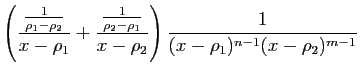 |
||
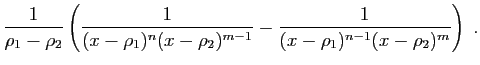 |
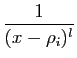 , où
, où
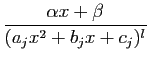 ,
où
,
où
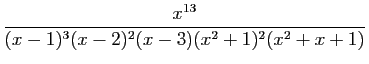 |
|||
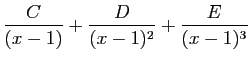 |
|||
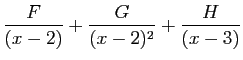 |
|||
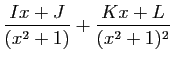 |
|||
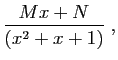 |
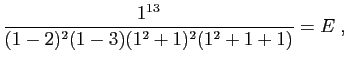
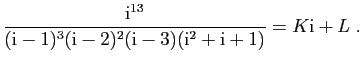
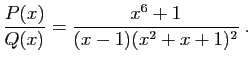
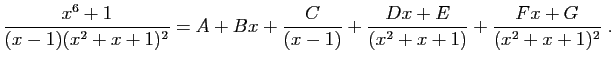
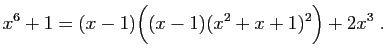
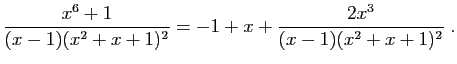
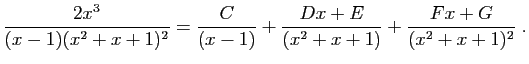
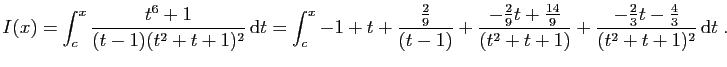
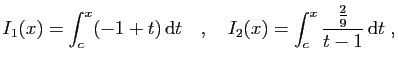
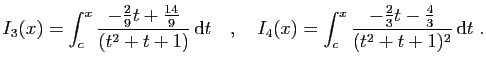
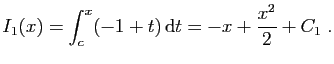
![$\displaystyle I_2(x) = \int_c^x \frac{\frac{2}{9}}{t-1} \mathrm{d}t =
\Big[\frac{2}{9}\ln\vert t-1\vert\Big]_c^x = \frac{2}{9}\ln\vert x-1\vert+C_2\;.
$](img324.gif)
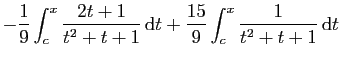 |
|||
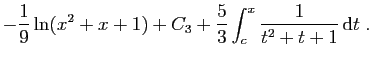 |
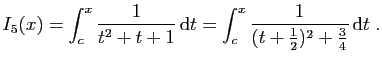
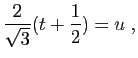 soit
soit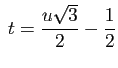 et
et 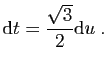
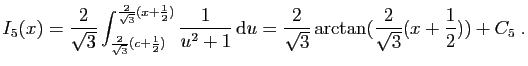
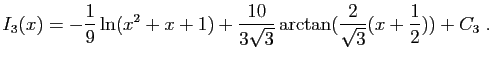
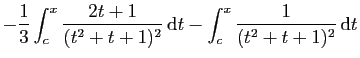 |
|||
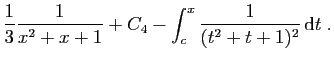 |
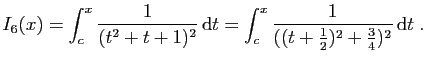
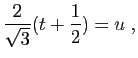 soit
soit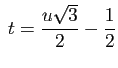 et
et 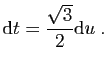
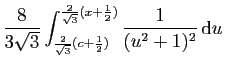 |
|||
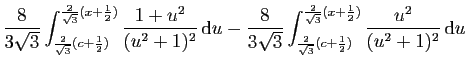 |
|||
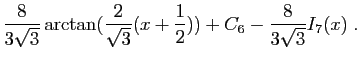 |
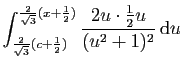 |
|||
![$\displaystyle \Big[-\frac{1}{u^2+1}\cdot(\frac{1}{2}u)
\Big]_{\frac{2}{\sqrt{3}...
...2})}^{\frac{2}{\sqrt{3}}(x+\frac{1}{2})}
\frac{\frac{1}{2}}{u^2+1} \mathrm{d}u$](img346.gif) |
|||
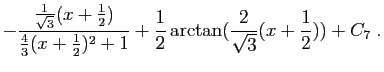 |
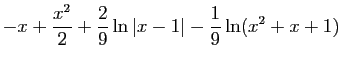 |
|||
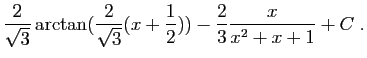 |
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales