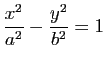 dans un repère orthonormal
dans un repère orthonormal
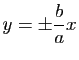 .
.
L'hyperbole d'équation
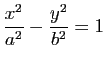 dans un repère orthonormal
dans un repère orthonormal
![]() admet comme asymptotes les droites d'équations
admet comme asymptotes les droites d'équations
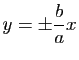 .
.
Son équation s'écrit encore
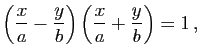
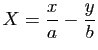 et
et
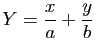 :
:
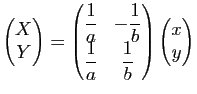
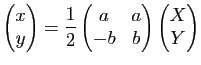
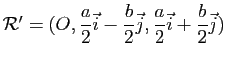 du point de coordonnées
du point de coordonnées
Plus généralement, une hyperbole admet, dans tout repère cartésien porté par ses asymptotes, une équation de la forme ![]() , pour un réel
, pour un réel ![]() non nul.
non nul.
Un tel repère n'est en général pas orthogonal. Il l'est si et seulement si l'hyperbole est équilatère.
Démonstration : Les asymptotes de l'hyperbole d'équation
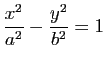 dans un repère orthonormal admettent comme vecteurs directeurs les vecteurs
dans un repère orthonormal admettent comme vecteurs directeurs les vecteurs ![]() et
et ![]() . Ces vecteurs sont orthogonaux si et seulement si
. Ces vecteurs sont orthogonaux si et seulement si ![]() , ou encore
, ou encore
![]() , puisque la demi-distance focale
, puisque la demi-distance focale ![]() vérifie
vérifie
![]() . Mais l'excentricité
. Mais l'excentricité ![]() est égale à
est égale à ![]() .
.![]()
Intersection de l'hyperbole et d'une droite
En utilisant l'équation de l'hyperbole dans un repère porté par les asymptotes, on vérifie immédiatement que toute droite parallèle à l'une des asymptotes (et distincte de cette asymptote) coupe l'hyperbole en exactement un point. Une telle droite admet en effet dans ce repère une équation de la forme ![]() ou
ou ![]() , où
, où ![]() (resp.
(resp. ![]() ) est un réel non nul.
) est un réel non nul.
Démonstration : Rapportons le plan à un repère (en général non orthonormé) porté par les asymptotes dans lequel l'équation de l'hyperbole est ![]() . Une droite
. Une droite ![]() non parallèle aux asymptotes a une équation de la forme
non parallèle aux asymptotes a une équation de la forme ![]() , avec
, avec ![]() . Un point de coordonnées
. Un point de coordonnées ![]() appartient à l'hyperbole et à
appartient à l'hyperbole et à ![]() si et seulement si
si et seulement si ![]() et
et
![]() . La droite
. La droite ![]() coupe donc l'hyperbole en deux points distincts
coupe donc l'hyperbole en deux points distincts ![]() et
et ![]() si le discriminant
si le discriminant
![]() de cette équation du second degré est strictement positif et un un point double s'il est nul. Dans le cas où
de cette équation du second degré est strictement positif et un un point double s'il est nul. Dans le cas où ![]() coupe l'hyperbole en deux points distincts ou confondus
coupe l'hyperbole en deux points distincts ou confondus ![]() et
et ![]() , le milieu du segment
, le milieu du segment ![]() a pour abscisse
a pour abscisse
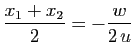 . Les points
. Les points ![]() et
et ![]() d'intersection de
d'intersection de ![]() avec les axes ont pour coordonnées
avec les axes ont pour coordonnées
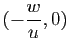 et
et
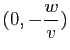 . Les milieux des segments
. Les milieux des segments ![]() et
et ![]() ont donc même abscisse et sont donc confondus, puisqu'ils appartiennent tous deux à
ont donc même abscisse et sont donc confondus, puisqu'ils appartiennent tous deux à ![]() .
.![]()
Construction de l'hyperbole point par point
On en déduit une construction point par point d'une hyperbole dont on connaît les asymptotes et un point : si ![]() est le point donné, on mène par
est le point donné, on mène par ![]() une droite coupant les asymptotes en
une droite coupant les asymptotes en ![]() et
et ![]() , le symétrique
, le symétrique ![]() de
de ![]() par rapport au milieu
par rapport au milieu ![]() du segment
du segment ![]() appartient alors à l'hyperbole. On peut ainsi construire à la règle et au compas autant de points de l'hyperbole qu'on le souhaite.
appartient alors à l'hyperbole. On peut ainsi construire à la règle et au compas autant de points de l'hyperbole qu'on le souhaite.
![\includegraphics[width=0.5\textwidth]{construction_hyperbole1}](img316.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales