Si 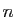 est un entier, ses diviseurs autres que lui-même sont dits propres :
est un entier, ses diviseurs autres que lui-même sont dits propres : 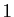 ,
, 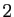 , et
, et 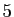 sont
les diviseurs propres de
sont
les diviseurs propres de 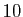 . On disait autrefois «partie aliquote», du mot latin signifiant «plusieurs fois».
Notons
. On disait autrefois «partie aliquote», du mot latin signifiant «plusieurs fois».
Notons 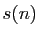 la somme des diviseurs propres de
la somme des diviseurs propres de 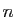 .
.
- Si
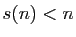 ,
, 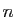 est dit déficient
est dit déficient
- Si
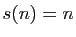 ,
, 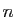 est dit parfait
est dit parfait
- Si
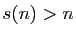 ,
, 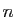 est dit excessif, excédent ou abondant
est dit excessif, excédent ou abondant
- Si
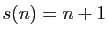 ,
, 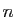 est dit quasi-parfait
est dit quasi-parfait
En bon successeur de Pythagore, Nicomaque de Gérase accompagne cette classification d'une interprétation symbolique
dans son «Introduction à l'arithmétique», au IIe siècle ap. J.C.
Il associe aux nombres abondants l'excès, l'ambition... et aux nombres déficients le manque, les défauts, la pauvreté, les nombres
parfaits étant parés de toutes les vertus :
Il arrive que, de même que le beau et le parfait sont rares et se comptent aisément, tandis que le laid et le mauvais sont
prolifiques, les nombres excédents et déficients sont en très grand nombre et en grand désordre ; leur découverte
manque de toute logique. Au contraire, les nombres parfaits se comptent facilement et se succèdent dans un ordre
convenable ; on n'en trouve qu'un seul parmi les unités, 6, un seul dans les dizaines, 28, un troisième assez loin
dans les centaines, 496 ; quant au quatrième, dans le domaine des mille, il est voisin de dix mille, c'est 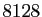 .
Ils ont un caractère commun, c'est de se terminer par un 6 ou par un 8, et ils sont tous invariablement pairs.
.
Ils ont un caractère commun, c'est de se terminer par un 6 ou par un 8, et ils sont tous invariablement pairs.
Il n'y a bien que 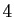 nombres parfaits inférieurs à
nombres parfaits inférieurs à 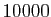 :
: 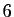 ,
, 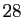 ,
, 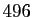 et
et 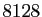 . La Proposition IX.36 des Éléments
d'Euclide affirme que tous les nombres de la forme
. La Proposition IX.36 des Éléments
d'Euclide affirme que tous les nombres de la forme
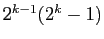 pour
pour
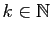 sont parfaits si
sont parfaits si 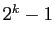 est premier :
sauriez-vous le démontrer ?
Le problème de la réciproque (tous les nombres parfaits sont-ils de cette forme ?) a été posé par Thabit ibn Qurra au IXe siècle,
Ibn al-Haytham vers l'an 1000, puis
par Descartes en 1638 dans une lettre à Mersenne,
puis par Franz van Schooten en 1658 dans une lettre à Fermat.
Ce n'est qu'en 1732
qu'Euler montre qu'il n'y a pas d'autre nombre parfait pair. On ignore toujours s'il y en a une infinité,
et s'il existe des nombres parfaits impairs : aucun n'a été trouvé jusqu'à
est premier :
sauriez-vous le démontrer ?
Le problème de la réciproque (tous les nombres parfaits sont-ils de cette forme ?) a été posé par Thabit ibn Qurra au IXe siècle,
Ibn al-Haytham vers l'an 1000, puis
par Descartes en 1638 dans une lettre à Mersenne,
puis par Franz van Schooten en 1658 dans une lettre à Fermat.
Ce n'est qu'en 1732
qu'Euler montre qu'il n'y a pas d'autre nombre parfait pair. On ignore toujours s'il y en a une infinité,
et s'il existe des nombres parfaits impairs : aucun n'a été trouvé jusqu'à 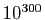 , mais qui sait ?
De même, on ignore toujours s'il existe des nombres quasi-parfaits.
Le plus petit nombre abondant impair est
, mais qui sait ?
De même, on ignore toujours s'il existe des nombres quasi-parfaits.
Le plus petit nombre abondant impair est 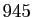 mais il en existe une infinité :
tout multiple strict d'un nombre parfait ou abondant est abondant.
Deux nombres
mais il en existe une infinité :
tout multiple strict d'un nombre parfait ou abondant est abondant.
Deux nombres 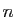 et
et 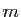 tels que
tels que 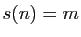 et
et 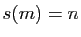 sont dits amicaux ou amiables.
Les nombres amicaux sont depuis très longtemps chargés d'une forte connotation symbolique.
Dans la Bible, Jacob donne deux cent chèvres et vingt boucs, et autant de brebis et de béliers à son
frère aîné Ésaü (pour éviter que celui-ci le tue...) ; pourquoi 220 ? On rapporte que Pythagore aurait qualifié un ami
d'«un autre lui, comme le sont 220 et 284». Ce couple de nombres amicaux
était apparemment le seul connu des Grecs, mais les Arabes en trouvèrent bien
d'autres. Thabit ibn Qurra (826-901) ouvrit la première voie systématique, en démontrant le résultat suivant.
sont dits amicaux ou amiables.
Les nombres amicaux sont depuis très longtemps chargés d'une forte connotation symbolique.
Dans la Bible, Jacob donne deux cent chèvres et vingt boucs, et autant de brebis et de béliers à son
frère aîné Ésaü (pour éviter que celui-ci le tue...) ; pourquoi 220 ? On rapporte que Pythagore aurait qualifié un ami
d'«un autre lui, comme le sont 220 et 284». Ce couple de nombres amicaux
était apparemment le seul connu des Grecs, mais les Arabes en trouvèrent bien
d'autres. Thabit ibn Qurra (826-901) ouvrit la première voie systématique, en démontrant le résultat suivant.
Soit 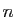 un entier supérieur à
un entier supérieur à 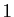 , et soient
, et soient
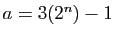 ,
,
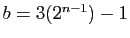 et
et
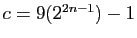 . Si
. Si 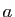 ,
, 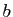 et
et 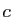 sont premiers,
alors
sont premiers,
alors 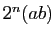 et
et 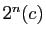 sont amicaux.
sont amicaux.
Al-Farisi (1260-1320) découvrit le couple
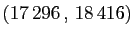 , Muhammad Baqir Yazdi le couple
, Muhammad Baqir Yazdi le couple
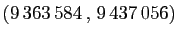 .
Comme souvent, ces résultats furent ignorés puis redécouverts par les Européens, et c'est ainsi que le couple d'Al Farisi porte le nom
de Fermat, celui de Yazdi le nom de Descartes, les nombres de la forme
.
Comme souvent, ces résultats furent ignorés puis redécouverts par les Européens, et c'est ainsi que le couple d'Al Farisi porte le nom
de Fermat, celui de Yazdi le nom de Descartes, les nombres de la forme 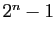 sont les nombres de Mersenne. Les nombres de la forme
sont les nombres de Mersenne. Les nombres de la forme 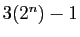 ont tout de même été nommés «nombres de Thebit», en
l'honneur de Thabit ibn Qurra.
ont tout de même été nommés «nombres de Thebit», en
l'honneur de Thabit ibn Qurra.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
. Ils ont un caractère commun, c'est de se terminer par un 6 ou par un 8, et ils sont tous invariablement pairs.
![]() un entier supérieur à
un entier supérieur à ![]() , et soient
, et soient
![]() ,
,
![]() et
et
![]() . Si
. Si ![]() ,
, ![]() et
et ![]() sont premiers,
alors
sont premiers,
alors ![]() et
et ![]() sont amicaux.
sont amicaux.
![]() , Muhammad Baqir Yazdi le couple
, Muhammad Baqir Yazdi le couple
![]() .
Comme souvent, ces résultats furent ignorés puis redécouverts par les Européens, et c'est ainsi que le couple d'Al Farisi porte le nom
de Fermat, celui de Yazdi le nom de Descartes, les nombres de la forme
.
Comme souvent, ces résultats furent ignorés puis redécouverts par les Européens, et c'est ainsi que le couple d'Al Farisi porte le nom
de Fermat, celui de Yazdi le nom de Descartes, les nombres de la forme ![]() sont les nombres de Mersenne. Les nombres de la forme
sont les nombres de Mersenne. Les nombres de la forme ![]() ont tout de même été nommés «nombres de Thebit», en
l'honneur de Thabit ibn Qurra.
ont tout de même été nommés «nombres de Thebit», en
l'honneur de Thabit ibn Qurra.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales