En el parrafo precedente, hemos visto como el test de Student permitía hacer un test sobre el efecto de un tratamiento comparando con un grupo de control. Podríamos querer evaluar los efectos de varios tratamientos diferentes. El análisis de varianza (analysis of variance o ANOVA) puede ser visto como una generalización del test de Student.
Se quiere hacer un test sobre los efectos de ![]() tratamientos que
han sido administrados a
tratamientos que
han sido administrados a
![]() individuos
respectivamente. En el análisis de varianza, el parámetro que
puede influir sobre los datos se llama un factor, y sus
valores las modalidades (en este caso los diferentes
tratamientos).
individuos
respectivamente. En el análisis de varianza, el parámetro que
puede influir sobre los datos se llama un factor, y sus
valores las modalidades (en este caso los diferentes
tratamientos).
En el modelo probabilista, cada modalidad corresponde a una
muestra. Para
![]() , denotamos por:
, denotamos por:
a las variables aleatorias que modelan los datos del ![]() -ésimo
grupo, que se suponen independientes y con una misma ley
-ésimo
grupo, que se suponen independientes y con una misma ley
![]() . Se supone que en particular la varianza
. Se supone que en particular la varianza
![]() es constante, hipótesis que puede ser validada a
través de un test.
es constante, hipótesis que puede ser validada a
través de un test.
Se quiere saber si la variabilidad que se observa en los datos se
debe solamente al azar o si existen efectivamente diferencias
significativas entre las clases, imputables al factor. Para esto
vamos comparar las varianzas empíricas de cada muestra con la
varianza de la muestra global, de tamaño
![]() . La
media de las varianzas (ponderada por los efectivos) resume la
variabilidad en el interior de las clases, de ahí el nombre de
varianza intra-clases o varianza
residual.
. La
media de las varianzas (ponderada por los efectivos) resume la
variabilidad en el interior de las clases, de ahí el nombre de
varianza intra-clases o varianza
residual.
La varianza de las medias describe las diferencias entre las clases que pueden deberse al tratamiento, de aquí el nombre de varianza inter-clases, o varianza explicada. Si los tratamientos tienen efectivamente un efecto, se espera que la varianza explicada sea grande en comparación con la varianza residual. La descomposición de la varianza de la muestra global en varianza explicada y varianza residual se da explícitamente en el siguiente resultado.
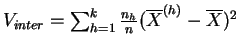 la varianza de las medias
(varianza inter-clases),
la varianza de las medias
(varianza inter-clases), 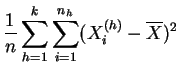 |
|||
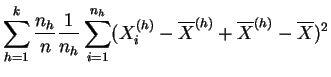 |
|||
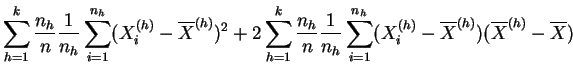 |
|||
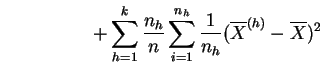 |
|||
El inciso 3 del teorema 3.1 permite cuantificar la ley de las diferentes componentes de la varianza, empleando el hecho que la suma de dos variables independientes que siguen dos leyes de chi-cuadrado sigue también una ley de chi-cuadrado, y que su cociente ponderado sigue una ley de Fisher. Los resultados son los siguientes.
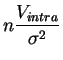 sigue la
ley de
chi-cuadrado
sigue la
ley de
chi-cuadrado
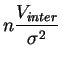 sigue la
ley de
chi-cuadrado
sigue la
ley de
chi-cuadrado
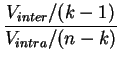 sigue la
ley de Fisher
sigue la
ley de Fisher
El
test ANOVA consiste entonces en rechazar la igualdad de las
medias (aceptar que hay un efecto de los tratamientos), cuando el
cociente ponderado entre la varianza explicada (inter-clases) y la
variance residual (intra-clases) es significativamente más grande
que los cuantiles de la ley
![]() .
Retomemos los datos sobre las tasas de colesterol en sangre del
parrafo precedente. El factor tiene dos modalidades. La
varianza explicada vale
.
Retomemos los datos sobre las tasas de colesterol en sangre del
parrafo precedente. El factor tiene dos modalidades. La
varianza explicada vale ![]() , la varianza residual
, la varianza residual ![]() . El
cociente ponderado de las dos es
. El
cociente ponderado de las dos es ![]() , con un
p-valor de:
, con un
p-valor de:
Es el doble del p-valor que habíamos encontrado para el test de
Student. En el caso de un análisis de varianza con dos
modalidades, el estadígrafo del test es el cuadrado del
estadígrafo del test de Student. Si una variable aleatoria sigue
la ley
![]() , su cuadrado sigue la ley
, su cuadrado sigue la ley
![]() . Efectuar un análisis de varianza o un test de
Student bilateral es estrictamente equivalente.
. Efectuar un análisis de varianza o un test de
Student bilateral es estrictamente equivalente.
Si el análisis de varianza acepta la hipótesis de
la igualdad de las esperanzas, el estudio está terminado. Pero
si
![]() es rechazada, podríamos desear ir más allá y
comparar los efectos de un factor, para subconjuntos de
modalidades, realizando análisis de varianza parciales.
es rechazada, podríamos desear ir más allá y
comparar los efectos de un factor, para subconjuntos de
modalidades, realizando análisis de varianza parciales.
Se puede presentar el análisis de varianza con un
factor desde un punto de vista ligeramente diferente. Escribamos
cada una de las variables aleatorias de la muestra relativa a la
![]() -ésima modalidad en la forma:
-ésima modalidad en la forma:
Esta presentación tiene la ventaja de aislar (en los
parámetros ![]() ) los efectos fijos de los factores. En
los casos en que las modalidades son muy numerosas o si los
tamaños de las muestras son muy pequeños, a veces se recurre a un
modelo de efectos aleatorios :
) los efectos fijos de los factores. En
los casos en que las modalidades son muy numerosas o si los
tamaños de las muestras son muy pequeños, a veces se recurre a un
modelo de efectos aleatorios :
Aunque el modelo sea diferente, el procedimiento es rigurosamente
idéntico.
El análisis de varianza se extiende
al estudio de los efectos de varios factores. Es la base de un
campo completo de la estadística, el diseño de
experimentos.