Valores de la esperanza y de la varianza

Las hipótesis de modelación son aquí más fuertes que en el capítulo precedente. Los datos observados se consideran como realizaciones de una muestra de la ley normal ${\cal N}(\mu,\sigma^2)$ cuya esperanza $\mu$ y varianza $\sigma^2$ son desconocidas. Bajo estas hipótesis, los resultados teóricos nos dicen que los estimadores naturales de $\mu$ y $\sigma^2$ son la media y la varianza empíricas.

Teorema 3.1 Sea $(X_1,\ldots,X_n)$ una muestra de la ley ${\cal N}(\mu,\sigma^2)$ . Denotamos :

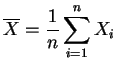$\bullet$: $\overline{X} = \displaystyle{\frac{1}{n} \sum_{i=1}^n X_i}$ la media empírica,
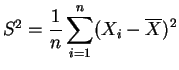$\bullet$: $S^2 = \displaystyle{\frac{1}{n} \sum_{i=1}^n (X_i-\overline{X})^2}$ la varianza empírica.

Entonces:

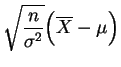$\displaystyle{\sqrt{\frac{n}{\sigma^2}}\Big(\overline{X}-\mu\Big)}$ sigue la ley normal ${\cal N}(0,1)$ .
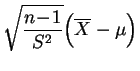$\displaystyle{\sqrt{\frac{n\!-\!1}{S^2}}\Big(\overline{X}-\mu\Big)}$ sigue la ley de Student ${\cal T}(n\!-\!1)$ .
$\displaystyle{\frac{nS^2}{\sigma^2}}$ sigue la ley de chi-cuadrado ${\cal X}^2(n\!-\!1)$ .

El inciso 1 permite hacer tests de hipótesis que tienen que ver con el valor de $\mu$ , cuando $\sigma$ es conocido. Es la situación típica de control de calidad. Consideremos una máquina destinada a fabricar comprimidos que deben pesar

gramo. Ningún comprimido, si se pesa con una sensibilidad del orden de microgramo, pesa exactamente

gramo. En promedio el peso de los comprimidos es

gramo, con una desviación estándar asociada a las características de la máquina que los fabrica, la cual es conocida (por ejemplo $\sigma = 0.01$ g). El control de calidad consistirá en tomar, cada cierto tiempo, una muestra de los comprimidos los cuales se pesarán exactamente. Se calculará su peso promedio para comprobar si existe una diferencia muy grande con el valor de referencia (

g). Por ejemplo, si en una muestra de

comprimidos se observa un peso promedio de

, el estadígrafo del test toma el valor de $\sqrt{10}(0.995-1)/0.01 = -1.581$ , y su p-valor con respecto a la ley normal ${\cal N}(0,1)$ es:

Si no se conoce la varianza, se puede emplear el inciso 2 de la misma forma. Retomemos los mismos datos, suponiendo que se ha observado una desviación estándar de

. El estadígrafo de test toma el valor $\sqrt{9}(0.995-1)/0.01 = -1.5$ , y su p-valor con respecto a la ley de Student ${\cal T}(9)$ es:

Se puede emplear el inciso 3 para hacer un test sobre el valor de la desviación estándar. Continuando con la muestra de

comprimidos supongamos que se observó una desviación estándar de

. Se quiere hacer un test para saber si este valor es significativamente más grande que el valor de referencia $\sigma = 0.01$ . El estadígrafo de test toma el valor

. Para la ley de chi-cuadrado ${\cal X}^2(9)$ , el p-valor correspondiente es:

Frecuentemente se plantea la hipótesis de normalidad, pero no siempre se puede hacer un test válido de la misma. En el caso de las muestras de gran tamaño, podemos obviar esto gracias al siguiente resultado, que una adaptación del Teorema del Límite Centrado.

Teorema 3.2 Sea $(X_1,\ldots,X_n)$ una muestra de una ley de probabilidad de esperanza $\mu$ y de varianza $\sigma^2$ finitas. Cuando

tiende a infinito, la ley de la variable aleatoria:

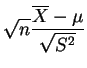
$\displaystyle \sqrt{n}\frac{\overline{X}-\mu}{\sqrt{S^2}}$

converge a la ley normal ${\cal N}(0,1)$ .

Este resultado se utiliza para realizar tests sobre los valores de la esperanza, exactamente igual que como se hizo con los incisos 1 y 2 del teorema 3.1.