Sección : Distribución empírica
Previo : Representaciones gráficas
Siguiente : Modelos probabilistas

Cuantiles

La función cuantil de una ley de probabilidad es la inversa (generalizada) de su función de distribución. Si $F$ denota la función de distribución, la función cuantil $Q$ es la función que a $u\in ]0,1[$ hace corresponder:

$$Q(u) = \inf\{x\;:\; F(x)\geq u\}\;.$$

La función cuantil empírica de una muestra es la función cuantil de su distribución empírica.

Definición 2.4   Sean $x=(x_1,\ldots,x_n)$ una muestra y $(x_{(1)},\ldots,x_{(n)})$ el vector de sus estadígrafos de orden. La función cuantil empírica de la muestra es la función $\widehat{Q}$ que , para todo $i=1,\ldots,n$, vale $x_{(i)}$ en el intervalo $]\frac{i-1}{n},\frac{i}{n}]$.

$$\forall u\in ]\frac{i-1}{n},\frac{i}{n}]\;,\quad \widehat{Q}(u) = x_{(i)}\;.$$

Para algunos valores de $u$, damos nombres particulares a los cuantiles $\widehat{Q}(u)$.

$u$	$\widehat{Q}(u)$
$0.5$	Mediana
$0.25$, $0.75$	Cuartiles
$0.1,\ldots,0.9$	Deciles
$0.01,\ldots,0.99$	Centiles

La mediana es el valor central de la muestra: hay tantos valores inferiores a ella como valores superiores a ella. Si la distribución empírica de la muestra es poco disimétrica, como por ejemplo para una muestra simulada a partir de una ley uniforme o normal, la media y la mediana están cercanas. Si la muestra es asimétrica, con una distribución muy dispersa hacia la derecha, la mediana podrá ser mucho más pequeña que la media. A diferencia de la media, la mediana no es sensible a los valores aberrantes. Ella satisface una propiedad de optimalidad con respecto a la desviación absoluta media.

Proposición 2.5   Sea $x=(x_1,\ldots,x_n)$ una muestra donde los $x_i$ son reales. Sea $EA$ (desviación absoluta) la función que a un número $m$ asocia:

$$EA(m) = \frac{1}{n} \sum_{i=1}^n \vert x_i - m\vert\;.$$

Esta función alcanza un mínimo absoluto para $m=\widehat{Q}(0.5)$ (la mediana). Al valor de este mínimo se le denomina desviación absoluta media.

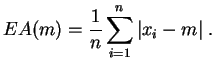
Demostración:  Para evitar complicar las notaciones, supondremos que los valores $x_i$ son todos diferentes. El gráfico de la función $EA$ está formado por segmentos de rectas. Sobre el intervalo $[x_{(i)},x_{(i+1)}]$, ella vale:

$$EA(m) = \frac{1}{n}\Big((2i-n) m -\sum_{j=1}^i x_{(j)}+ \sum_{j=i+1}^n x_{(j)}\Big)\;.$$

La pendiente $(2i\!-\!n)/n$ es primero negativa (para $i\leq n/2$), y después positiva (para $i>n/2$). Si $n$ es impar la mediana $\widehat{Q}(0.5)=x_{(\frac{n-1}{2})}$ es el único mínimo. Si $n$ es par, el mínimo se alcanza en todo el intervalo $[x_{(\frac{n}{2})},x_{(\frac{n}{2}+1)}[$, que contiene a $\widehat{Q}(0.5)$ y en el cual la pendiente se anula. $\square$

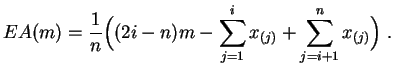
Hay algo arbitrario en la definición de la función cuantil para una distribución empírica: para todos los puntos del intervalo $[x_{(i)},x_{(i+1)}[$, la función de distribución vale $i/n$. Son sobre todo razones teóricas las que nos hacen seleccionar a $x_{(i)}$ en lugar de otro punto como valor de $\widehat{Q}(i/n)$. Puede ser una selección bastante mala en la práctica. Consideremos la muestra siguiente, de tamaño $6$.

$$1\,,\;2\,,\;3\,,\;7\,,\;8\,,\;9\;.$$

La mediana, tal y como la hemos definido, vale $3$. Sin embargo como valor central se impone claramente el punto medio del intervalo $[3,7]$, es decir $5$. En el caso de las muestras de tamaño par, el intervalo $[x_{(\frac{n}{2})},x_{(\frac{n}{2}+1)}[$, se llama intervalo mediano. A veces la mediana se define como el punto medio del intervalo mediano.

Este problema se presenta en el caso de muestras pequeñas y para los cuantiles $\widehat{Q}(u)$ en los cuales $u$ es de la forma $i/n$ (más frecuente la mediana). Nosotros no lo tomaremos en cuenta y conservaremos la definición 2.4. Aún en muestras muy grandes, los cuantiles son poco complicados de calcular, pues es suficiente ordenar la muestra en orden creciente para calcular sus estadígrafos de orden y por tanto a la vez obtener todos los cuantiles. Ellos nos proveen una visualización fácil de la distribución empírica. Hemos visto que la mediana es un valor central. Para medir la dispersión, podemos calcular el recorrido, que es la diferencia entre el mayor y el menor valor. Pero este recorrido refleja más los valores extremos que la localización de la mayor parte de los valores. Comprendemos mejor la dispersión de una muestra por los intervalos inter-cuartiles e inter-deciles.

Definición 2.6     Llamamos intervalo inter-cuartiles al intervalo $[\widehat{Q}(0.25), \widehat{Q}(0.75)]$, el cual contiene la mitad central de los valores de la muestra. Llamamos intervalo inter-deciles al intervalo $[\widehat{Q}(0.1), \widehat{Q}(0.9)]$, el cual contiene $80\%$ de los valores de la muestra.

Estos intervalos forman la base de una representación muy compacta de la distribución empírica: el diagrama en caja (o caja y bigotes, box plot, box-and-whisker plot). No existe una definición general de esta representación. Ella consiste en una caja rectangular cuyos dos extremos son los cuartiles. Estos extremos se prolongan por trazos que terminan con segmentos ortogonales (los bigotes). La longitud de estos segmentos varía según el autor. Nosotros proponemos fijarlos en los deciles extremos. Representamos también la mediana por un trazo en la caja y a veces se representan también los valores extremos de la muestra. (ver la figura 8).

Gráfico 9: Estaturas de niños de 6 años. La zona sombreada corresponde a el intervalo inter-cuartiles. La mediana está en trazo continuo, los deciles $\widehat{Q}(0.1)$ y $\widehat{Q}(0.9)$ en punteado.

Sección : Distribución empírica
Previo : Representaciones gráficas
Siguiente : Modelos probabilistas