Sección : Datos bidimensionales
Previo : Cociente de apuestas
Siguiente : Ejercicios

Tabla de contingencia

La tabla de contingencia es un medio particular de representar simultáneamente dos carácteres observados en una misma población, si son discretos o continuos reagrupados en clases. Los dos carácteres son $x$ e $y$, el tamaño de la muestra es $n$. Las modalidades o clases de $x$ se escribirán $c_1,\ldots,c_r$, las de $y$, $d_1,\ldots,d_s$. Se denota:

$\bullet$

$n_{hk}$ el efectivo conjunto de $c_h$ y $d_k$ : es el número de individuos para los cuales $x$ toma el valor $c_h$ e $y$ el valor $d_k$,

$\bullet$

$n_{h\bullet}=\sum_{k=1}^s n_{hk}$ el efectivo marginal de $c_h$ : es el número de individuos para los cuales $x$ toma el valor $c_h$,

$\bullet$

$n_{\bullet k}=\sum_{h=1}^r n_{hk}$ el efectivo marginal de $d_k$ : es el número de individuos para los cuales $y$ toma el valor $d_k$.

Se representan estos valores en una tabla de doble entrada, llamada tabla de contingencia:

$$\begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert... ...n_{\bullet k}&\ldots&n_{\bullet s}&n\\ \hline \end{array}$$

Cada fila y cada columna corresponden a una submuestra particular. La fila de índice $h$ es la distribución en $d_1,\ldots,d_s$, de los individuos para los cuales el carácter $x$ toma el valor $c_h$. La columna de índice $k$ es la distribución sobre $c_1,\ldots,c_r$, de los individuos para los cuales el carácter $y$ toma el valor $d_k$. Dividiendo las filas y las columnas por sus sumas, obtenemos en cada una, distribuciones empíricas formadas por frecuencias condicionales. Para $h=1,\ldots,r$ y $k=1,\ldots,s$, las denotaremos:

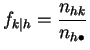$$f_{k\vert h} = \frac{n_{hk}}{ n_{h\bullet}}$$   y$$\quad f_{h\vert k} = \frac{n_{hk}}{ n_{\bullet k}}\;.$$

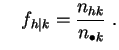
Estas distribuciones empíricas condicionales se llaman los perfiles-fila y perfiles-columna. La cuestión es estudiar la dependencia de los dos carácteres. Dos carácteres son independientes si el valor de uno no influye sobre la distribución de los valores del otro. Si este es el caso, los perfiles-fila diferirán muy poco de la distribución empírica de $y$, y los perfiles-columna de la de $x$ :

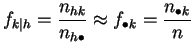$$f_{k\vert h} = \frac{n_{hk}}{n_{h\bullet}}\approx f_{\bullet k} = \frac{n_{\bullet k}}{ n}$$   y$$\quad f_{h\vert k} = \frac{n_{hk}}{n_{\bullet k}}\approx f_{h\bullet} = \frac{n_{h\bullet}}{n}\;.$$

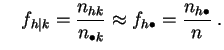
Es equivalente a decir que las frecuencias conjuntas deben estar cerca de los productos de las frecuencias marginales:

$$f_{hk} = \frac{n_{hk}}{n} \approx f_{h\bullet}\, f_{\bullet k} =\frac{n_{h\bullet}}{n}\,\frac{n_{\bullet k}}{n}\;.$$

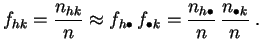
Las frecuencias conjuntas por un lado, y los productos de las frecuencias marginales por el otro, constituyen dos distribuciones de probabilidad sobre el conjunto producto $\{c_1,\ldots,c_r\}\times\{d_1,\ldots,d_s\}$. Una de las maneras de cuantificar su proximidad es calcular la distancia de chi-cuadrado de una con respecto a la otra. En este caso particular, hablamos de chi-cuadrado de contingencia.

Proposición 3.9   La distancia de chi-cuadrado de contingencia de la distribución empírica $(f_{hk})$ a la distribución teórica $(f_{h\bullet}f_{\bullet k})$ vale:

$$D_{\chi^2} = \sum_{h=1}^r\sum_{k=1}^s \frac{(f_{hk} -f_{h\bullet}\, f_{\bullet k})^2 }{f_{h\bullet}\,f_{\bullet k}}$$

$$= -\!1+\sum_{h=1}^r\sum_{k=1}^s \frac{n_{hk}^2}{n_{h\bullet}\, n_{\bullet k}}\;.$$

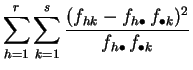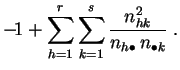Demostración:  La primera expresión es la aplicación directa de la definición 2.7. Para pasar a la segunda, se desarrolla el cuadrado.

$$D_{\chi^2} = \sum_{h=1}^r\sum_{k=1}^s \frac{f_{hk}^2 }{f_{h\bullet}\,f_{\bulle... ...=1}^r\sum_{k=1}^s f_{hk} + \sum_{h=1}^r\sum_{k=1}^s f_{h\bullet}\,f_{\bullet k}$$

$$= \sum_{h=1}^r\sum_{k=1}^s \frac{f_{hk}^2 }{f_{h\bullet}\,f_{\bullet k}} \;-2\;+1$$

$$= -\!1+\sum_{h=1}^r\sum_{k=1}^s \frac{n_{hk}^2}{n_{h\bullet}\, n_{\bullet k}}\;.$$

$\square$

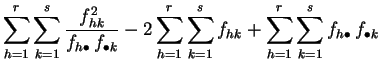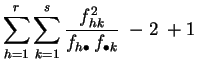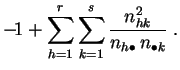La distancia de chi-cuadrado vale 0 si los dos carácteres son independientes. Ella es máxima si existe una dependencia sistemática. Supongamos que $r\!=\!s$ y $y\!=\!f(x)$, para una cierta función biyectiva $f$. En cada fila y en cada columna de la tabla de contingencia una sola casilla es diferente de cero y la distancia de chi-cuadrado vale $(r\!-\!1)$.

Sección : Datos bidimensionales
Previo : Cociente de apuestas
Siguiente : Ejercicios