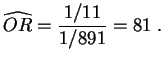Cociente de apuestas

Este parrafo trata únicamente el caso de dos carácteres binarios, indicadores de dos eventos diferentes, de los cuales deseamos estudiar la dependencia. Es un caso que encontramos en medicina cada vez que se plantea el problema de una detección terapéutica. Denotemos por

(por enfermedad) al primer evento y

(por síntoma) al segundo. El síntoma puede ser una tasa elevada de una cierta substancia o la reacción positiva a un test de detección, como un test de alcoholemia. En cada individuo de una población de tamaño

, se observan la presencia o la ausencia de la enfermedad y del síntoma. Tenemos entonces los

resultados posibles siguientes:

El problema es extraer de estos datos una base para un diagnóstico: ¿con qué certeza podemos anunciar a una persona que está enferma, si se ha encontrado el síntoma en ella? En otras palabras, ¿podemos dar un valor a la probabilidad de que un individuo esté enfermo sabiendo que presenta el síntoma? Esta probabilidad teórica, denotada $\mathbb {P}[E\,\vert\,S]$ , se llama el valor positivo predictivo del síntoma. Podemos relacionarla con otras cantidades por la fórmula de Bayes:

$\displaystyle \mathbb {P}[E\,\vert\,S] = \frac{\mathbb {P}[S\,\vert\,E]\; \mat... ...b {P}[E]+\mathbb {P}[S\,\vert\,\overline{E}] \;\mathbb {P}[\overline{E}]}\;.$

La probabilidad $\mathbb {P}[E]$ , que representa la proporción de enfermos en la población es, frecuentemente, muy débil y difícil de estimar de manera fiable. Una de las razones es que la enfermedad se detecta solamente entre las personas que van a una consulta médica, y por lo tanto no son representativos del conjunto de la población. En el ejemplo del test de alcoholemia, de hecho es imposible definir la proporción de individuos que han bebido demasiado, pues ella depende de la hora del día, del lugar, etc... Las probabilidades condicionales del síntoma sabiendo la enfermedad son en general las únicas accesibles.

Definición 3.7 Llamamos:

$\bullet$: sensibilidad a la probabilidad $\mathbb {P}[S\,\vert\,E]$ (probabilidad que un individuo enfermo presente el síntoma),
$\bullet$: especificidad la probabilidad $\mathbb {P}[\overline{S}\,\vert\,\overline{E}]$ (probabilidad que un individuo no enfermo no presente el síntoma).

En un caso ideal, estas dos cantidades deberían valer

. Una prueba de alcoholemia debería dar positiva en todo individuo que ha bebido demasiado, y nunca acusar erróneamente a un conductor sobrio. En la práctica, la sensibilidad y la especificidad son inferiores a

, con diferencias importantes según las pruebas. Si se trata de una enfermedad sin tratamiento conocido, puede ser más grave alarmar erróneamente a una persona no enferma, que el no detectar a una persona que lo está. Se preferirán tests con una especificidad muy fuerte, aunque su sensibilidad no sea tan buena. Y el inverso para una enfermedad potencialmente grave, pero fácilmente curable, se emplearán tests de sensibilidad fuerte.

Una sensibilidad fuerte y una especificidad fuerte no garantizan que el valor positivo predictivo sea bueno, si la proporción de enfermos es pobre. Supongamos por ejemplo $\mathbb {P}[S\,\vert\,E]=\mathbb {P}[\overline{S}\,\vert\,\overline{E}]=0.9$ y $\mathbb {P}[E] = 0.01$ . De acuerdo con la fórmula de Bayes el valor positivo predictivo vale:

$\displaystyle \mathbb {P}[E\,\vert\,S] = \frac{0.9\;\,0.01}{0.9\;\,0.01 + 0.1\;\,0.99} = \frac{1}{12}\;.$

Concretamente, en

personas que presentan el síntoma,

no están enfermos. Si nos detenemos en esta cifra, parece inquietante, pero si calculamos también $\mathbb {P}[E\,\vert\,\overline{S}]$ , obtenemos

. La proporción de enfermos entre los individuos que presentan el síntoma es de hecho mucho más fuerte que entre los que no presentan el síntoma. Diremos que el síntoma está a favor de la enfermedad. Se plantea entonces el problema de evaluar la eficiencia del síntoma en la detección de la enfermedad, por un número que no depende de $\mathbb {P}[E]$ .

Para esto empleamos el cociente de apuestas o proporción de probabilidades (odds-ratio en inglés). El cociente de apuestas (en el sentido que tiene odds en inglés para los apostadores) de un evento es la proporción de la probabilidad del evento en relación a la de su complementario. La ''apuesta'' de la enfermedad puede calcularse entre los individuos que presentan el síntoma ( $\mathbb {P}[E\,\vert\,S]/\mathbb {P}[\overline{E}\,\vert\,S]$ ) y entre los que no lo tienen ( $\mathbb {P}[E\,\vert\,\overline{S}]/\mathbb {P}[\overline{E}\,\vert\,\overline{S}]$ ). El cociente de apuestas teórico es la razón de estas dos cantidades.

$\displaystyle OR = \frac{\mathbb {P}[E\,\vert\,S]/\mathbb {P}[\overline{E}\,\ve... ...ne{S}]}{ \mathbb {P}[\overline{E}\cap S]\,\mathbb {P}[E\cap\overline{S}]}\;.$

El cociente de apuestas vale

si la enfermedad y el síntoma son independientes, es mayor que

si el síntoma está a favor de la enfermedad. Cuando se han realizado observaciones sobre una muestra, podemos aproximar las probabilidades teóricas por frecuencias empíricas. Esto lleva a la definición de cociente de apuestas empírico.

Definición 3.8 Se llama cociente de apuestas empírico a la cantidad:

$\displaystyle \mathop{\widehat{OR}} = \frac{n_{ES}\, n_{\overline{E}\,\overline{S}} }{ n_{\overline{E}S}\,n_{E\overline{S}}}\;.$

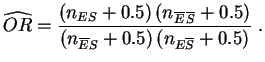
$\displaystyle \widehat{OR} = \frac{(n_{ES}+0.5)\, (n_{\overline{E}\,\overline{S}}+0.5) }{ (n_{\overline{E}S}+0.5)\,(n_{E\overline{S}}+0.5)}\;.$

Ejemplo: Supongamos que para una muestra de

individuos, La distribución sea la siguiente:

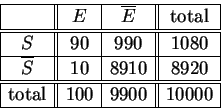
$\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert\vert c\vert} ... ...e\hline \mbox{total}&100&9900&10000\\ \hline \end{array} \end{displaymath}$

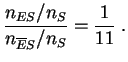
$\displaystyle \frac{n_{ES} / n_S}{n_{\overline{E}S} / n_S} = \frac{1}{11}\;.$

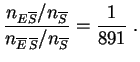
$\displaystyle \frac{n_{E\overline{S}} / n_{\overline{S}} }{ n_{\overline{E}\,\overline{S}} / n_{\overline{S}}} = \frac{1}{891}\;.$

Por cada enfermo hay

no enfermos entre los individuos que no presentan el síntoma. El cociente de apuestas empírico vale: