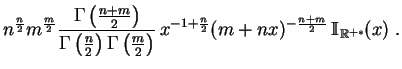![$\displaystyle \mathbb {P}[X\in A] = \int_A f_X(x)\,dx\;.
$](img344.gif)
La ley de la variable aleatoria ![]() es la ley continua sobre
es la ley continua sobre
![]() , de densidad
, de densidad ![]() .
.
![$\displaystyle \mathbb {P}[X\in A] = \int_A f_X(x)\,dx\;.
$](img344.gif)
La ley de la variable aleatoria ![]() es la ley continua sobre
es la ley continua sobre
![]() , de densidad
, de densidad ![]() .
.
Para determinar la ley de una variable
aleatoria continua, hay que calcular su densidad. De manera
equivalente, la ley de una variable continua se determina dando la
probabilidad de que ella pertenezca a un intervalo ![]() cualquiera.
Es lo que hemos hecho para nuestro ejemplo de base, el llamado a
Random, que es una variable aleatoria continua, de densidad
cualquiera.
Es lo que hemos hecho para nuestro ejemplo de base, el llamado a
Random, que es una variable aleatoria continua, de densidad
![]() .
Una variable aleatoria continua
.
Una variable aleatoria continua
![]() de densidad
de densidad ![]() , cae entre
, cae entre ![]() y
y ![]() con una probabilidad
igual a :
con una probabilidad
igual a :
![$\displaystyle \mathbb {P}[a<X < b]=\int_{a}^b\,f_X(x)\,dx\;.
$](img348.gif)
Mientras más grande sea la densidad ![]() en un segmento, mayores
serán las probabilidades de que
en un segmento, mayores
serán las probabilidades de que ![]() caiga en ese segmento, lo cual
justifica el término ``densidad''.
caiga en ese segmento, lo cual
justifica el término ``densidad''.
Como ya hemos observado para Random, la probabilidad de que una variable aleatoria continua caiga en un punto cualquiera es nula.
![$\displaystyle \mathbb {P}[X=a] = \int_{\{a\}} f_X(x)\,dx = 0\;.
$](img349.gif)
Observemos también que el modificar una densidad en un número
finito o numerable de puntos, no cambia de las integrales sobre
los segmentos y en consecuencia la ley de probabilidad asociada
tampoco cambia. El valor que toma la densidad en un punto
particular, no es importante. Por ejemplo Random tiene como
densidad a
![]() pero da lo mismo usar
pero da lo mismo usar
![]() .
Como en los casos discretos, debemos conocer
algunos ejemplos básicos. Las densidades se dan en un punto
cualquiera de
.
Como en los casos discretos, debemos conocer
algunos ejemplos básicos. Las densidades se dan en un punto
cualquiera de
![]() .
.
La ley uniforme
sobre un intervalo es la ley de ``sorteos al azar'' en un
intervalo. Si ![]() son dos números reales, la ley uniforme sobre
el intervalo
son dos números reales, la ley uniforme sobre
el intervalo ![]() se denota por
se denota por
![]() . Ella tiene por
densidad a la función:
. Ella tiene por
densidad a la función:
![$\displaystyle \frac{1}{b-a}\mathbb {I}_{[a,b]}(x)\;.
$](img355.gif)
Las leyes
exponenciales modelan intervalos de tiempo o duraciones aleatorias, como
la vida de una partícula en física. La ley exponencial de
parámetro
![]() se denota por
se denota por
![]() . Ella tiene por densidad a
la función:
. Ella tiene por densidad a
la función:
La ley
normal, ley de Gauss o Laplace-Gauss es la más célebre de las
leyes de probabilidad. Su éxito y su omnipresencia en las ciencias
de la vida vienen del Teorema del Límite Centrado que estudiaremos
más adelante. La ley normal de parámetros
![]() y
y
![]() se denota por
se denota por
![]() . Ella
tiene por densidad a la función:
. Ella
tiene por densidad a la función:
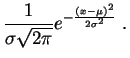
Las leyes exponenciales y normales constituyen
el núcleo de las familias de leyes clásicas que se encuentran mas
frecuentemente en estadística.
La ley de Weibull
de parámetros ![]() y
y ![]() , denotada por
, denotada por
![]() , tiene por densidad:
, tiene por densidad:
La ley gamma de parámetros ![]() y
y
![]() , denotada por
, denotada por
![]() tiene por
densidad:
tiene por
densidad:
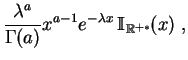
La ley beta de
parámetros ![]() y
y ![]() , denotada por
, denotada por
![]() tiene por
densidad:
tiene por
densidad:
![$\displaystyle \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}
x^{a-1}(1-x)^{b-1}\mathbb {I}_{]0,1[}(x)\;.
$](img378.gif)
Esta familia de leyes nos provee de modelos no uniformes para
variables aleatorias acotadas. Si unas variables aleatorias
independientes siguen la ley uniforme
![]() , sus
estadígrafos de orden (valores reordenadas) siguen leyes beta.
, sus
estadígrafos de orden (valores reordenadas) siguen leyes beta.
La ley log-normal
![]() es
la ley de una variable aleatoria, de valores positivos, cuyo
logaritmo sigue la ley
es
la ley de una variable aleatoria, de valores positivos, cuyo
logaritmo sigue la ley
![]() . Ella tiene por
densidad a la función:
. Ella tiene por
densidad a la función:
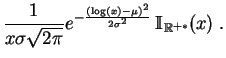
La ley de Student
con ![]() grados de libertad,
grados de libertad,
![]() , es la ley de la
relación
, es la ley de la
relación
![]() , donde las variables aleatorias
, donde las variables aleatorias ![]() e
e ![]() son independientes,
son independientes, ![]() de ley
de ley
![]() ,
, ![]() de ley
de ley
![]() . Ella tiene por densidad a la función:
. Ella tiene por densidad a la función:
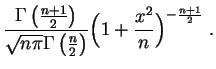
La ley de Fisher de parámetros ![]() y
y ![]() (enteros positivos) es la ley de la relación
(enteros positivos) es la ley de la relación
![]() , donde
, donde
![]() e
e ![]() son dos variables aleatorias independientes de leyes
son dos variables aleatorias independientes de leyes
![]() y
y
![]() respectivamente. Ella tiene por
densidad a la función:
respectivamente. Ella tiene por
densidad a la función: